First of all, the above program is traversing the list from the end and checks whether any node is less than the prev. min or greater than the prev. max ... if it lies between pev. min and prev. max then it returns 0.
Pre-Order traversal of BST -
1. Root.
2. Left.
3. Right.
.So, Pre-order traversal of BST will contain elements like - root, ....., left, ...., right .. ...
And we know that in a case of BST, left < root < right.
Now, if any node has two children then while traversing the pre-order from the back end, the program will return 0 when it will be traversing that particular node( with two children), because, before that point, we must have been traversed its both the left and right child. And since the current node element is neither less than prv. min ( if(a[i] < min) ----false)..nor it is greater than prev. max. ( else if (a[i] > max ----- false) and will go into else block and will return 0.
Example -
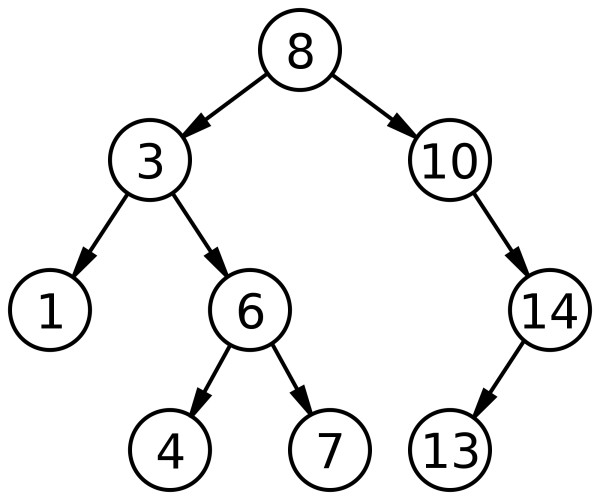
Pre-order - a [] = { 8, 3 , 1, 6 , 4 , 7 , 10 , 14, 13 }
now while trav. from back side- max =14 , min =13
when we reach at node 6 ( which has two children). [ index =3 from start=0 ].
min =4 and max =14.
where 6 is neither less than the prev min = 4 nor greater than prev max = 14. Hence will return 0.
Example- 2- BST with at max 1 child to any node.
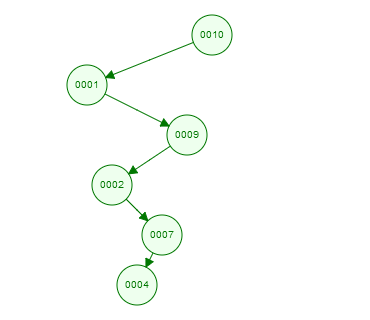
Pre- order traversal - a[ ] = { 10, 1, 9, 2, 7, 4].
Now traverse from back end-
max= 7, min=4.
now every time it will satisfy if(a[i] < min) and else if(a[i] > max) alternatively. Hence finally will return 1.
If it is Inorder instead of preorder - The above program would always return 1. [ inorder traversal gives sorted list.]
If it is postorder then also it will always return 1 for all BST. [ work on it ].