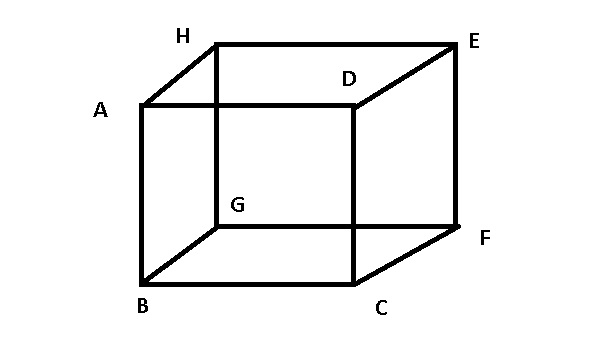
The modified diagram is as above.
Now, you can choose opposite faces at any moment for perfect matching.
Let the faces be:
CFED - face 1
AHGB - face 2
ADCB - face 3
HEFG - face 4
BGCF - face 5
AHED - face 6
Lets say I choose face 1 and face 2 then there are 4 ways to do perfect matching:
DE and CF and HG and AB.
DE and CF and AH and BG.
DC and EF and HG and AB.
DC and EF and AH and BG.
Similarly, for face 3 and face 4 taken together.
Similarly, for face 5 and face 6 taken together.
So, total = 12 perfect matchings (some have been counted more than once)
We will now eliminate matchings that have been counted more than once.
BG and CF and AH and DE have been counted in face 1 and face taken together as well as face 5 and face 6 taken together.
HG and EF and AB and CD have been counted in face 1 and face 2 taken together as well as face 3 and face 4 taken together.
GF and BC and HE and AD have been counted in face 5 and face 6 taken together as well as face 3 and face 4 taken together.
So, we will make 3 matching less from total.
$\therefore$ Total perfect matchings possible = 12 - 3 = 9