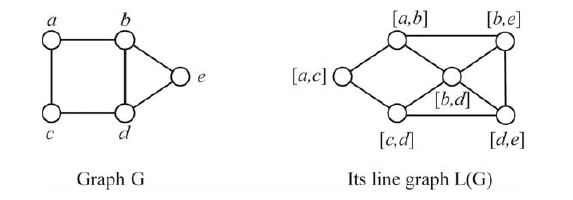
L(G) is a 2-set {e1,e2} of edges in G with which are adjacent to a common vertex v. This vertex v is uniquely determined by {e1,e2}.
If a vertex vv has degree d, there are (d2) 2-sets{e1,e2} such that e1 and e2 are adjacent to v
So the total number of edges in L(G) is
$\sum_{i=0}^{n}\binom{n}{2}=n(n-1)/2$
There is very simple and easy proof to drive expression for number of edges in lines graph-


