Consider $n=3$, we have $9$ vertices in the plane. The vertices are:
$(1,1),\quad(1,2),\quad (1,3), \quad (2,1),\quad (2,2),\quad (2,3),\quad (3,1),\quad (3,2),\quad (3,3)$
So, the corresponding graph will be:

Minimum spanning tree:
(One of the possibilities)

There is no problem with a minimum spanning tree. We have $n^{2}$ vertices, so the minimum spanning tree contains $n^{2}- 1$ edges of cost $1$. So, the cost of the minimum spanning tree is $n^{2}-1$.
Maximum spanning tree:
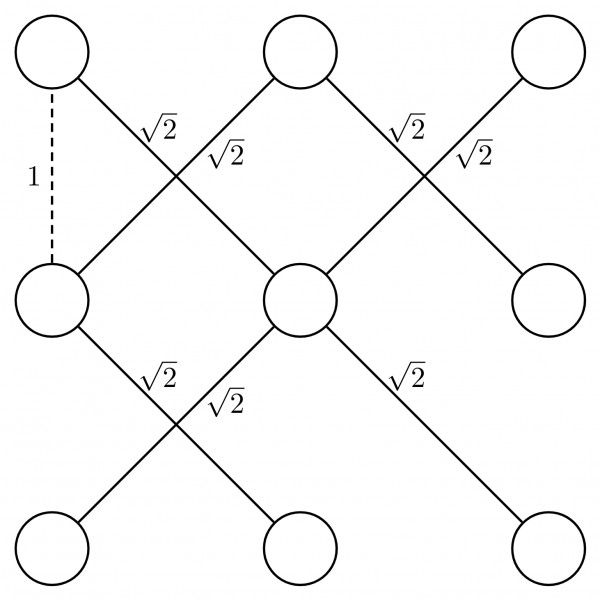
In this maximum spanning tree of $n^{2}$ $-$$ 1$ edges , $n^{2}$ $-$$ 2$ edges are of cost ${\sqrt{2}}$ and $1$ edge is of cost $1$.
So, the answer is ${\sqrt{2}}$ $\left ( n{^{2}}-2 \right )+1$.
This pattern continues for high values of $n.$
For $n=4$, the maximum spanning tree is:
(one of possibilities)
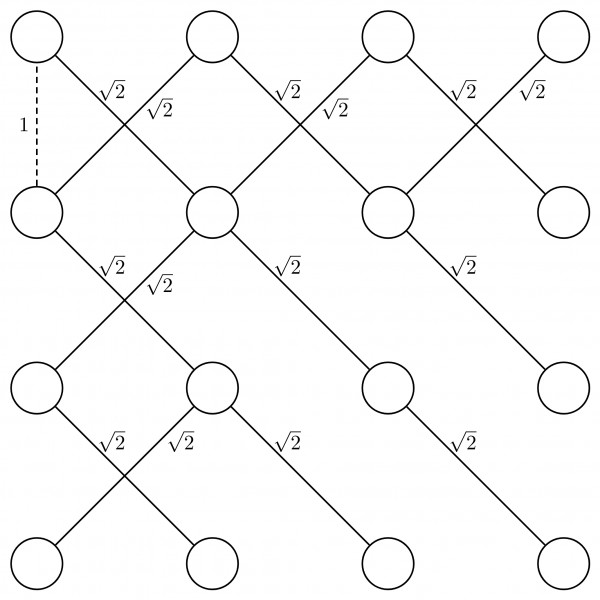
For $n=4$ , $16$ vertices are there and the maximum spanning tree requires $15$ edges. Out of $15$ edges, $14$ edges are of cost ${\sqrt{2}}$ and $1$ edge is of cost $1$. Thus satisfying the formula ${\sqrt{2}}$ $\left ( n{^{2}}-2 \right )$ $+1$.
The cost of Minimum spanning tree is: $n^{2}-1$.
The cost of Maximum spanning tree is: $\left ( n^{2}-2 \right )\sqrt{2}+1$.