.Okay let's say I assign the minimum weight possible as from the inequality given in the question to the edges in the graph I get the below graph

Now using kruskal method I start forming the MST
(1)First I choose edge AE with weight -2.
(2)Then Edge BD(3)
(3)Then Edge BF(3)
(4)Then Edge CF(4)
At this state, I have my graph as
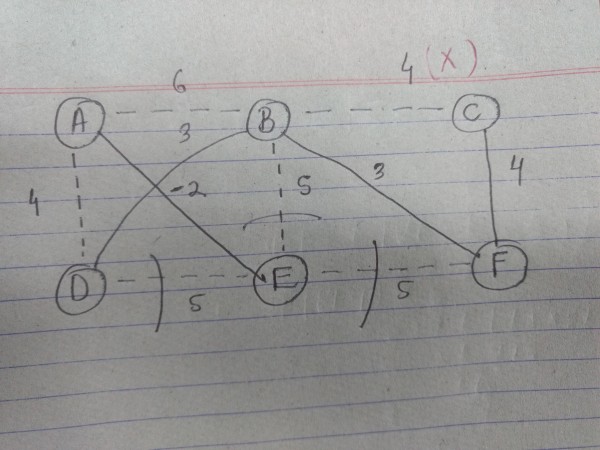
Now my graph has two disconnected components namely AE and BDCF.
I won't use edge BC because it would form a cycle. So I will reject this.
Now I can choose to join these two components with either edge AD(4), BE(5),DE(5),EF(5),AB(6).
We note that the edge DE was included in MST which means the next least value weight edge available to my kruskal algorithm was 5 and not 4, otherwise edge AD would have been chosen. And since I had a choice, so I took any one of BD,BE or EF and made my MST. So cost of BD,BE,EF is fine.
Hence, the cost of AD must not be atleast 4. Infact cost of AD $\geq 5$
Answer-(D)