CMI2012-B-02b

Question

For a binary string $x = a_0a_1 \dots a_{n−1}$ define $val(x)$ to be $\Sigma_{0 \leq i < n} 2^{n-1-i}.a_i$
Let $\Sigma = \{(0, 0),(0, 1),(1, 0),(1, 1)\}$.

• A. Construct a finite automaton that accepts exactly those strings $(a_0, b_0)(a_1, b_1) \dots (a_{n−1}, b_{n−1}) \in  \Sigma^*$ such that $val(b_0b_1 \dots b_{n−1}) = 4 · val(a_0a_1 \dots a_{n−1})$.

Answer 1

Before analysing this problem , please have a look at my answer for the problem : https://gateoverflow.in/46562/cmi2012-b-02a .

This problem is a slight modification to the problem that I mentioned above. But the idea of construction of FA completely differs for this problem.

Analysing the input string:

Consider the input: $01011010$

$(a0 a1 a2 a3)$ $=$ $0011$

$(b0 b1 b2 b3)$ $=$ $1100$

val$(b0 b1 b2 b3)$ $=$ $4$ . val$(a0 a1 a2 a3)$

So this input is one of the strings belonging to the language.

For any string belonging to this language, the least significant $2$ bits of $($$b0$ $b1$ $b2$ $b3$....$bn$$-$$1$$)$  should be zeros because val$($$b0$ $b1$ $b2$ $b3$$)$ $=$ $4$ . val($a0$ $a1$ $a2$ $a3$$)$. [Any bit sequence which is a multiple of 4 will end with 00]

The $2$ most significant bit positions of  $($$a$0 $a1$ $a2$ $a3$.......$an-1$$)$ should be zeros so only there exists a possibility for $($$b0$ $b1$ $b2$ ....$bn-1$$)$ to be $4$ times the value of  $($$a0$ $a1$ $a2$ $a3$.......$an$$-$$1$$)$.

These are the $2$ basic requirements for the input to be a part of the language.

Idea of construction of Finite Automaton :

Consider the input  01011010

$(a0 a1 a2 a3)$ $=$ $0011$

$(b0 b1 b2 b3)$ $=$ $1100$

We can clearly see from the above example that  

$a0=a1=0$

$b0=a2$

$b1=a3.$

$b2=b3=0$

For any input in the language,

$a0=a1=0$

$b0=a2$

$b1=a3$

$b2=a4$

......

$bn-3 =an-1$

$bn-2=bn-1=0$

So, this input pattern should have to recognized by the Finite automaton.

The corresponding Finite automaton is:

 

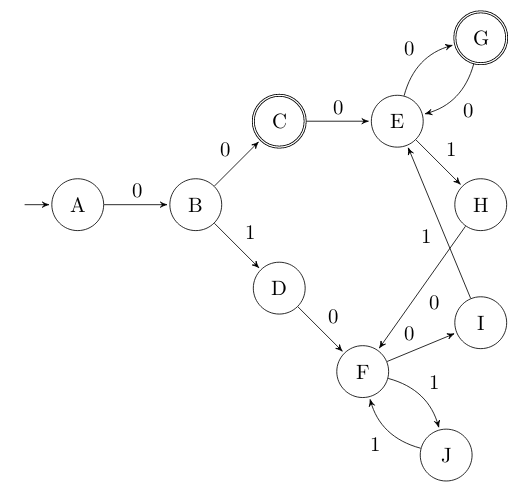
Regular Expression :  $00 +  (000+010(11)^*01).(00+10(11)^*01)^*.0$

Comments

@verma ashish transition on (11) at q1 is missing , should lead to dead state.
Here relevance of each state is like even no. of 0s even no. of 1's , odd no of 0s and Odd no. of 1's ?

---

@punit

Yes there will be a transition to dead state..

---

can somebody explain how did you form the regular expression?