Yes. It can be done in the following way,
Explanation :
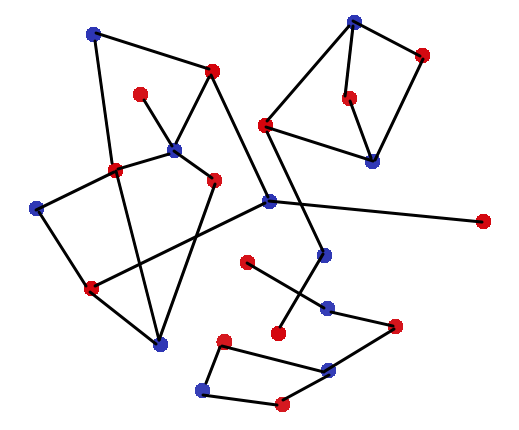
- Above is a bipartite graph
- If we crawl through the graph using dfs , one step at a time and verify the nodes for different colors, then we will find that this graph is indeed bipartite.
- So, obviously why not crawl through an uncolored graph and color it one - by- one node and flipping the color every alternatively. we can definitely do it , if the graph is indeed bipartite.
Logic:
// set bipartite flag as true initially
bool flag = true;
void dfs(int u,int color){
// if unvisited node
if(!visited[u]) {
visited[u] = true; // mark as visited
node_color[u] = color; // color this node u with color
// checking all nodes in the row of u in the matrix
for ( all v :: an adjacent vertices of u) {
// do the following
if ( there is an edge between u and v){ // edge between v and u
// if color of vertex v is equal to color of u,
// then we are not able to color any further
if (color of v:adjacent == my_color(u) ) {
// graph is not bipartite so return
set bipartite flag as zero (false)
return from this dfs;
}
// flip the color and continue dfs
if (adjacent: v is not visited) {
// recurse dfs again
dfs(v,opposite_color);
}
}
}
}
}
How will it detect odd length cycle?
In the following way,

Actual Implementation:
// graph represented using adjacentcy matrix
#include <iostream>
#include <vector>
#include <stdio.h>
using namespace std;
bool b_flag = true;
// V = max_nodes
int V;
// color can be 0 or 1
//.............................................................................................
// main dfs function
void dfs(int u,int color,std::vector<std::vector<bool>> adj,int visited[],int node_color[]){
if(!visited[u] && b_flag) {
visited[u] = true;
node_color[u] = color; // color this node u with color
// checking all nodes in the row of u in the matrix
for (int v = 0; v < V; v++) {
if ( adj[u][v] == 1){ // edge between v and u
// if color of vertex v is equal to color of u,
// then we are not able to color any further
if (node_color[v] == color) {
// graph is not bipartite so return
b_flag = false;
return;
}
// flip the color and continue dfs
if (!visited[v]) {
dfs(v,(color == 1)?0:1,adj,visited,node_color);
}
}
}
}
}
//.............................................................................................
int main(int argc, char const *argv[]) {
// enter you no of vertices
scanf("%d",&V);
// declare required variables and arrays
// adjacency matrix use for graph representation
// node_color[V] will store the color
// of every vextices while coloring
// vector are used for random access
// and to avoid all those pointer casting problems
std::vector<std::vector<bool>> adj(V, std::vector<bool>(V));
int node_color[V];
for(int m = 0;m<V;m++) node_color[m] = -1; // initial node colors -1 = uncolored
int visited[V] = {0}; // all are unvisited nodes now
// initialize the matrix
for(int i=0;i<V;i++) {
for(int j=0;j<V;j++) {
adj[i][j] = 0;
}
}
// matric initialization done !
//.....................................
// scan through the input file
// and develop the adjacency matrix
// node numbers are starting from index 0 to V-1
int u,v;
while(scanf("%d %d",&u,&v) != EOF) {
// read one line of input
// read two nodes
//scanf("%d %d",&u,&v);
// u and v have a bidirectional edge between them
adj[u][v] = adj[v][u] = 1;
}
//......................................
// use a color variable
// actually boolean type can be used
// for color
//printf("Hi3\n");
int color;
//....................................
// call dfs() now
// using for loop here to handle disconnected graph as well
// after completing one dfs tree
// we must need to jump
// to another tree
int node = 0;
for(int node=0;node<V;node++) {
color = 1;
dfs(node,color,adj,visited,node_color);
// count ++;
// We can use this counter to count
// the the no of connected componentes..//
// For connected graph this dfs call
// will invoke only once from here .. //
// For disconnected graph
// dfs will be invoked count times
// from this for loop
}
//printf("Hi4\n");
// ...............................
// checking the flag now
if(b_flag) {
printf("G is bipartite\n");
}else {
printf("G is not bipartite\n");
}
return 0;
}
compile: g++ -std=c++11 bipartite.cpp
input file:
- First line contains
No of vertices
- Remaining lines should contain vertices pairs representing one
bi-directional edge
- Vertex indices starts from
0 to V-1
// input.txt
7
0 1
0 2
1 3
3 2
4 5
6 4
5 6
Execute :a.exe < input.txt
O/P : G is not bipartite