Look at how heap and stack sections are incorporated in the Runtime Environment.
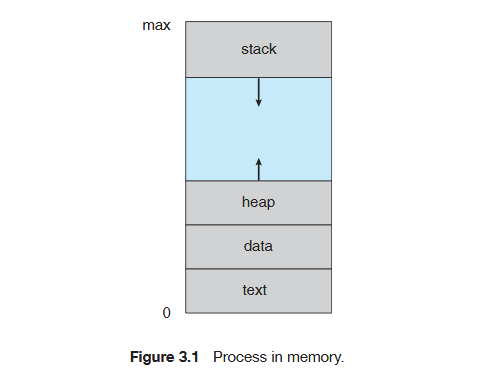
That is the most efficient way to utilize the space. If we divide the space by half, what if one entity requires 60% of the space, while the other entity requires none? Halving the available space is an inefficient way to utilize it.
Efficient utilization would be to let a stack take up all the space if the other stack doesn't want it.
For the array [1...MaxSize] Let top1 point to 0, and top2 point to MaxSize+1 in the beginning, since both the stacks are empty.
Stack full will be when:-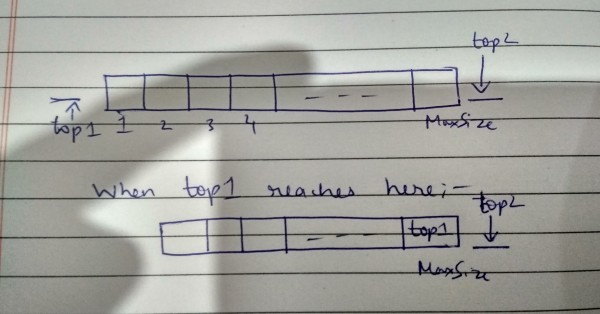
Option D