Ans A)
As there is no match between x and y element, and we could tell no of element in x= no of elements in y
So, we we can tell it is an even digit string
Other than this we cannot assume anything
So, it should be a regular language of even length
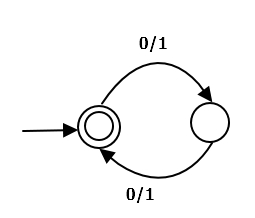
NFA should be like this
$S->1S0 | 0S1|\epsilon$
no of element in x= no of elements in y that part is regular
x!=y this part is CFL
Concatenation of this two will be give ans
CFL$\cap$Regular=CFL
ans will be CFL