- $3x+2y=14\rightarrow(1)$
- $2x−3y=5\rightarrow(2)$
To get the intersection point, we solve the equations and get $x=4,y=1$
We can draw the required area like this
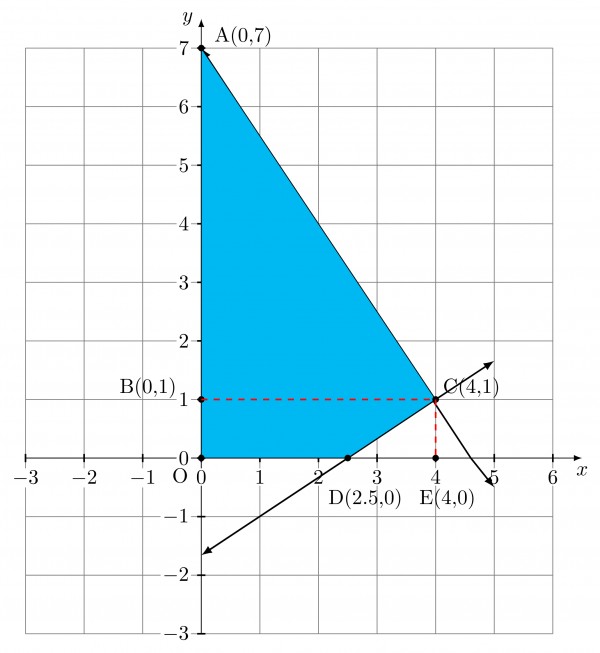
From the above diagram,
Area $=\triangle ABC +\Box OBCE-\triangle CDE$
Area $=\left(\dfrac{1}{2}\times 4\times 6\right)+\left(1\times 4\right)-\left(\dfrac{1}{2}\times\dfrac{3}{2}\times 1\right)$
Area $=12+4-\dfrac{3}{4}=16-0.75=15.25$
So, the correct answer is $(B).$