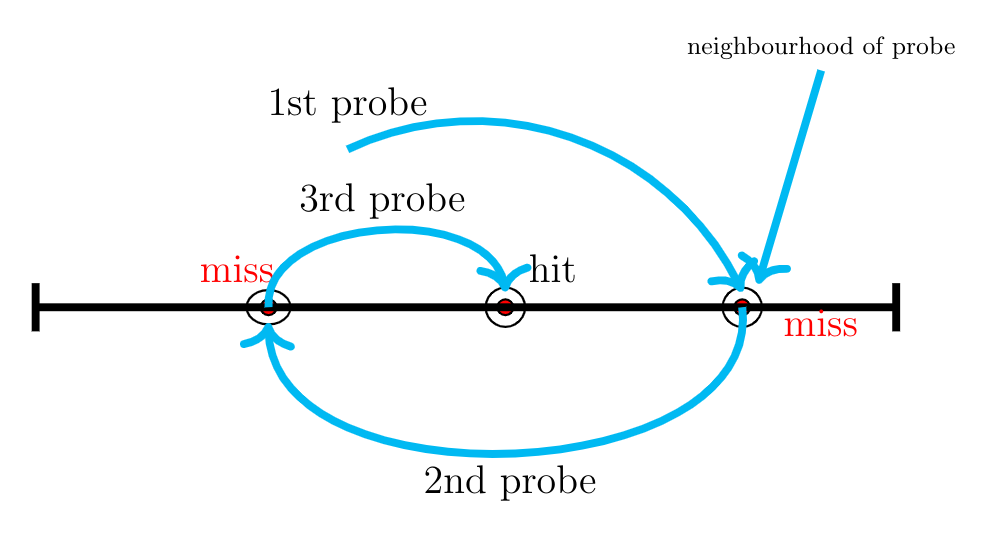
It should not take more than 5 probes
#include <bits/stdc++.h>
using namespace std;
#define N 100
void display(bool a[]) {
int i=0;
while(i<31) printf("%2d ",a[i++]);
}
void assign(bool a[],int zeros) {
for(int i=0;i<31;i++)
(i<zeros)?a[i] = 0:a[i] = 1;
}
int main() {
srand(time(NULL));
bool a[31];
// header
for(int i=0;i<31;i++) printf("%2d ",i);
printf("\n\n");
int max_probes = 0;
for(int iteration = 1;iteration <= N;iteration++) {
int zeros = rand()%32;
assign(a,zeros);
sort(a,a+31);
int low,high,mid,ans;
std::vector<int> seq;
low = 0;
high = 31;
while(low < high) {
mid = low + floor((high - low) / 2);
seq.push_back(mid);
if(a[mid] == 0) {
low = mid + 1;
ans = low;
if(a[mid + 1] == 1) break;
} else {
high = mid;
ans = high;
if(mid > 0)
if(a[mid - 1] == 0) break;
}
}
display(a);
printf(" | probes=%d ",seq.size());
for(auto e:seq) printf("%d ",e);
printf(" | at = %dth\n",ans);
//if(ans == 15) printf("\nHHH=-------------\n");
max_probes = max(max_probes,(int)(seq.size()));
seq.clear();
}
printf("%d\n",max_probes);
}