To create the Huffman tree, always increase the nodes in ascending order, and merge the first two nodes.
Step 1)
Given: $\begin{bmatrix} P & Q &R &S &T \\ 0.22 &0.34 &0.17 &0.19 &0.08 \end{bmatrix}$ → $\begin{bmatrix} T & R &S &P &Q \\ 0.08 &0.17 &0.19 &0.22 &0.34 \end{bmatrix}$ → $\begin{bmatrix} TR &S &P &Q \\ 0.25 &0.19 &0.22 &0.34 \end{bmatrix}$
Step 2)
$\begin{bmatrix} TR &S &P &Q \\ 0.25 &0.19 &0.22 &0.34 \end{bmatrix}$ → $\begin{bmatrix} S &P&TR &Q \\ 0.19 &0.22 &0.25 &0.34 \end{bmatrix}$ → $\begin{bmatrix} SP&TR &Q \\ 0.41 &0.25 &0.34 \end{bmatrix}$
Step 3)
$\begin{bmatrix} SP&TR &Q \\ 0.41 &0.25 &0.34 \end{bmatrix}$ → $\begin{bmatrix} TR&Q &SP \\ 0.25 &0.34 &0.41 \end{bmatrix}$ → $\begin{bmatrix} TRQ &SP \\ 0.59 &0.41 \end{bmatrix}$
Step 4)
Finally merge these two.
Hence, the Huffman Tree would look like this:-
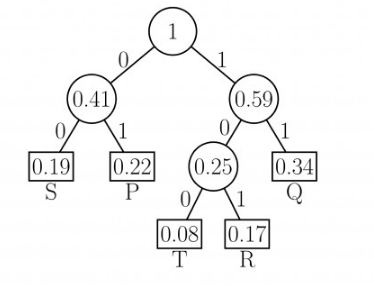
$(0.22*2)+(0.34*2)+(0.19*2)+(0.17*3)+(0.08*3)=2.25$
Length 2.25 per character. Given, there are 100 characters in the message, so,
$2.25*100=225$
225