Let $f(x)=e^x+0.5x^2-2$, and we want to see if $f(x)=0$ has any solution in $\left [ -5, 5 \right ]$
$f'(x)$ = $e^x+x$ and we definitely have solution of $f'(x)=0$ in $\left [ -5, 5 \right ]$ because $f'(x)$ is continuous and $f'(-5) \lt 0$, $f'(5) \gt 0$
(Moreover $f'(x)$ has only one solution as it is a strictly increasing function.)
Let $k$ be one of the solutions for $f'(x)$ hence $f'(k) = 0$ where $k \in [-5, 5]$, for $\text{“}\lt k\text{”}, f'(x)$ is $-$ve and for $\text{“}\gt k\text{”}, f'(x)$ is $+$ve. means for $\lt k$, $f(x)$ is decreasing and for $\gt k, f(x)$ is increasing.
Rough plot of $f(x)$ may go like this
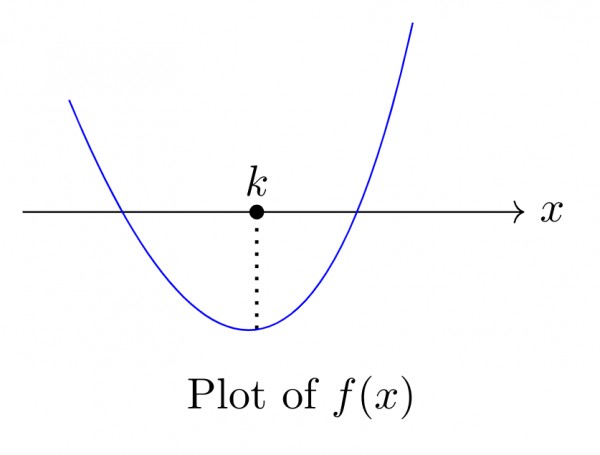
Now it is clear that $f(x)$ has two solutions.
BUT, how can i sure that these solutions are in between $[-5, 5]$ ?
Yes I agree that $k \in [-5, 5]$, but there are many possibilities of solution to be in $[-5, 5]$



(in all three images $k \in [-5, 5]$)
You wanna know which image is correct ? :O
Just check sign of $f(-5)$ and $f(5)$, u will get to know "Image-$1$" is correct one.
Hence, there are $2$ solutions in between of $[-5, 5]$.
C is correct answer.