$\text{Some Mathematical Preliminaries to answer this question}$
- Partition P* is a refinement of the partition P if P* covers P i.e. every point of P is a point of P*.
- Take a Partition of a line P1 and P2 as
- $a_{0}$ $a_{1}$ $a_{2}$ $a_{3}$...$a_{n}$
- $b_{0}$ $b_{1}$ $b_{2}$ $b_{3}$…...$b_{n}$ respectively
- Now consider a line L having both P1 $\cup $ P2 on L
- i.e. L has all the points $a_{0}$ $a_{1}$ $a_{2}$ $a_{3}$...$a_{n}$ ,$b_{0}$ $b_{1}$ $b_{2}$ $b_{3}$…...$b_{n}$
If P1 and P2 are two different partitions of the interval [a,b] then P* = p1 $\cup$ P2 is the common refinement of P1,P2
$Now$ $we$ $are$ $eligible$ $to$ $answer$ $this$ $question$
$Given: $ S is partitioned into 4 sets $\pi_{1}$, $\pi_{2}$, $\pi_{3}$ and $\pi_{4}$ given below.
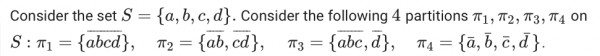
$Solution:$
As per our knowledge on refinement, we can say that,
$\pi_{1}$ = {abcd}
$\pi_{2}$ = {ab,cd}
$\pi_{3}$ = {abc,d}
$\pi_{4}$= {a,b,c,d}
Now, let us draw the Hassey Diagram for the relationship between these partitions.
Imagine the elements as the different colored boxes, in order to understand the beauty of mathematics :)