We have two sets : one is having 8 elements and another one is having 9 elements. (sets representing the schools here)
We are interested in two particular element x and y (for example in place of Rebecca and Elise)
These two elements $(x,y)$ belong to different sets. Allocate them in any order in those two sets (schools are indistinct, therefore we need not swap $x$,$y$ and simulate the following process again)
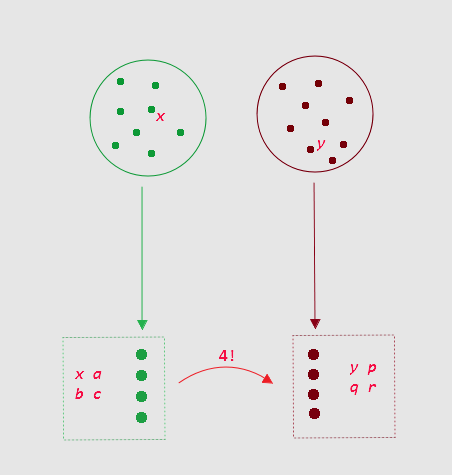
After selecting $4$ elements from each set we can map $(x,a,b,c)$ to $(y,p,q,r)$ in $4!$ ways in a one-to-one and onto mapping. These $4!$ ways also include $3!$ ways in which $x$ is always mapped to $y$ and $3*3!$ ways in which $x$ is never mapped to $y$.
(a).
probability that (x,y) pair results at the end =
$\begin{align*}
\left [ \text{probability of x getting selected} \right ] \cdot \left [ \text{probability of y getting selected} \right ] \cdot \left [ \text{probability of getting (x,y) pair} \right ]
\end{align*}$
=
$\begin{align*}
\left [ \frac{7C3}{8C4} \right ] \cdot \left [ \frac{8C3}{9C4} \right ] \cdot \left [ \frac{3!}{4!} \right ] = \frac{1}{18} \\
\end{align*}$
(b).
probability that (x,y) pair does not result at the end =
$\begin{align*}
\left [ \frac{7C3}{8C4} \right ] \cdot \left [ \frac{8C3}{9C4} \right ] \cdot \left [ \frac{3*3!}{4!} \right ] = \frac{1}{6} \\
\end{align*}$