The answer is C
It is very clear from the diagram that q3 is unreachable. Hence it can be removed.
After its removal the diagram looks like
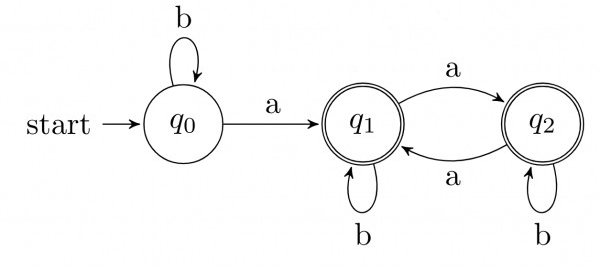
Based on Arden’s Theorem of converting DFA to Regular Expression,
It states that,
Let P and Q be two regular expressions over ∑.
If P does not contain a null string ∈, then,
R = Q + RP has a unique solution i.e. R = QP*
STEPS for constructing REGEX
- Form equation for each state and add ∈ in the initial state equation
- Bring final state in the form of R = Q + RP
In case of having multiple final state,
1. Write Regex for each final state and add them all to arrive at the final solution
For the above problem,
q0 = q0.b + ∈ → 1 (Epsilon is added as part of step 1)
q1 = q0.a + q1.b + q2.a -→ 2
q2 = q1.a + q2.b → 3
Now Compare equation 1 with R = Q+RP , (R = q0 ; Q= ∈ ; P = b)
thus q0 = ∈ . b*
q0 = b*
Substituting q0 value in equation 1, we get
q1 = b*.a + q1.b + q2.a → 4
Since our problem contains two final state add the two state to arrive at the final solution
ADD equation 2 and 4
q1 + q2 = b*.a + q1.b + q2.a + q1.a + q2.b
q1 + q2 = b*.a + q1(a + b) + q2 (a+b)
q1 + q2 = b*.a + (q1 + q2)(a+b) → 5
Compare equation 5 with R = Q+RP , (R = q1 + q2 ; Q= a.b* ; P = (a+b) )
Thus,
q1+q2 = b*.a(a+b)* ///// R = Q + RP has a unique solution i.e. R = QP*