For a regular graph how much large the value of degree (for each vertices) should be such that the graph is $2$ - connected. (vertex wise).
I did in this way :
$\begin{align*} &\quad \kappa(G) \leq \frac{2\cdot e}{n} \qquad \text{ where } \kappa(G) = \text{ vertex connectivity } \\ &\Rightarrow 2 \leq \frac{2\cdot e}{n} \\ &\Rightarrow n \leq e \\ &\Rightarrow n \leq \frac{\sum \left ( d_i \right )}{2} \\ &\Rightarrow n \leq \frac{n \cdot d}{2} \\ &\Rightarrow d \geq 2 \\ \end{align*}$
The above case can be realized by thinking of a cycle graph of $n$ vertices.
But in the following case :
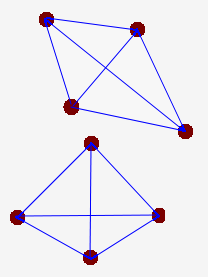
This graph is 3 regular and not 2- connected although $d \geq 2$ is satisfied.
Why this $d \geq 2$ is trivial and not working in some cases ?