Assumptions:
- by 'graph' I mean a simple graph.
- $n$ = no. of vertices in a graph.
- $e$ = no. of edges in a graph.
Definitions:
- Matching - it is a set of non-adjacent edges of a graph.
- Perfect Matching - it is a matching which matches every vertex with some other vertex in the graph. Perfect matching can't exist for graphs containing odd no. of vertices, because one unmatched vertex will always be left.
- Matching Number - it is the size of the largest matching of a graph.
- Covering (or Edge Cover or Line Cover) - it is a set of edges (adjacent or non-adjacent) such that every vertex of the graph is covered by at least one edge in that set. Covering can't exist for graph containing one or more isolated vertices.
- Covering Number - it is the size of the smallest covering of a graph.
Answer:
You think right. It is not possible for a graph to have the same Matching and Covering numbers without having a Perfect Matching.
The points (1) and (2) below, show that the Matching Number and Covering Number of a graph can be same only when both are equal to $\frac{n}{2}$. And, the points (3) and (4) show that if the Matching Number and Covering Number of a graph are both equal to $\frac{n}{2}$, then there will always exist AT LEAST one set of edges which is both a Perfect Matching as well as a Covering.
- When an edge joins two vertices, the two vertices of the edge are matched to each other.
- What can be the minimum no. of edges in a Matching ?
- A set containing a single edge is always a matching as there is no other edge in the set to which it can be adjacent to.
- What can be the maximum no. of edges in a Matching ?
- A matching set can have a maximum of $\left \lfloor \frac{n}{2} \right \rfloor$a non-adjacent edges because if even one more edge is further added then that edge will become adjacent to some edge already present in the set, and the set will no more be a matching.
- Therefore, $1$ $\leq$ $Matching$ $Number$ $\leq \left \lfloor \frac{n}{2} \right \rfloor$
- Similarly, when an edge joins two vertices, both the vertices are said to be covered.
- What can be the maximum no. of edges in a Covering ?
- Since there is no restriction on the adjacency of edges in a Covering and the edge set (of a graph with no isolated vertices) always covers all the vertices, the edge set of a graph is always a Covering. Hence, the size of a Covering can't exceed $e$.
- What can be the minimum no. of edges in a Covering ?
- Since a single edge covers only two vertices and there are a total of $n$ vertices to be covered, therefore a minimum of $\left \lceil \frac{n}{2} \right \rceil$b edges is necessary to form a Covering.
- Therefore, $\left \lceil \frac{n}{2} \right \rceil \leq$ $Covering$ $Number$ $\leq e$.
- In a graph where $n$ is even, if there exists a Matching of size $\frac{n}{2}$, then the Matching Number of the graph is $\frac{n}{2}$ because it can't exceed $\frac{n}{2}$. And, the Matching itself becomes a Perfect Matching because the $\frac{n}{2}$ non-adjacent edges in the matching, together, match and pair every vertex of the graph with some other vertex of the graph. Also, since a Perfect Matching matches every vertex with some vertex, all the vertices of the graph are covered. Therefore, every Perfect Matching is a Covering.
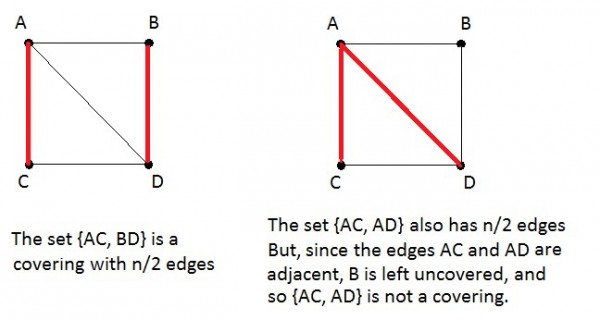
- If a Covering contains $\frac{n}{2}$ edges, and $n$ is even, then the Covering number of the graph is $\frac{n}{2}$ as it can't be smaller any more. Also, the $\frac{n}{2}$ edges of such a Covering will always be non-adjacent to each other, because otherwise (as shown in the below figure) it wouldn't then be possible to cover all the $n$ vertices and at least one vertex would be left uncovered. Therefore, given that $n$ is even, every Covering of $\frac{n}{2}$ edges is a Perfect Matching.
a The maximum no. of edges possible in a Matching is "floor" of $\frac{n}{2}$ because if there are even no. of vertices then all of them can be matched using $\frac{n}{2}$ non-adjacent edges, but if there are odd no. of vertices then only $n-1$ vertices can be matched and paired using $\frac{n-1}{2}$ non-adjacent edges. So, we generalize and combine both the cases by saying that the max. possible no. of edges in a Matching is $\left \lfloor \frac{n}{2} \right \rfloor$.
b The minimum no. of edges possible in a Covering is "ceiling" of $\frac{n}{2}$ because if there are even no. of vertices then $\frac{n}{2}$ edges can cover all of them, but if there are odd no. of vertices then only $n-1$ vertices can be covered using $\frac{n-1}{2}$ edges. One more edge will be needed to cover the remaining uncovered vertex, thus requiring a total of $\frac{n-1}{2}+1=\frac{n+1}{2}$ edges for the Covering. So, to generalize, we say that min. possible no. of edges in a Covering is $\left \lceil \frac{n}{2} \right \rceil$.