Number of vertices are 3, maximum edges possible in this graph is C(3,2) = 3
Necessary condition for two graphs to be isomorphic is
1) They have same no of vertices
2) They have same no of edges
3) They have same degree sequence
4) They must preserve adjacency
We have 3 edges to make graph, so we have possible choices to draw no edge, 1 edge, 2 edge or 3 edge.
Graph with no edge:

Only 1 non isomorphic graph is possible.
Graph with 1 edge
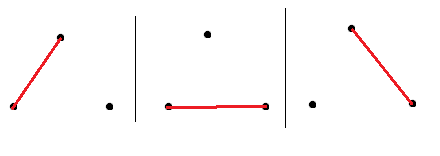
But all three graphs are isomorphic to each other(satisfying above conditions), so only 1 non isomorphic graph is possible.
Graph with 2 edges
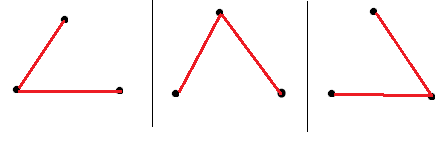
Similarly, these are also isomorphic to each other, so only 1 non isomorphic graph is possible
Graph with 3 edge
This is a complete graph of 3 vertices
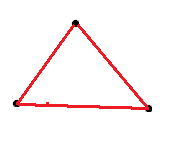
Only 1 non isomorphic graph is possible.
In total there are 1+1+1+1 = 4 non isomorphic graphs possible with 3 vertices
Hence 4 should be the correct answer