Bisection method is exactly like binary search on a list.
In bisection method, in each iteration, we pick the mid point of the interval as approxiamation of the root, and see where are we, i.e. should we choose left sub-interval, or right-subinterval, and we continue until we find the root, or we reach some error tolerance.
So in first iteration, our guess for root is mid point of [1,9] i.e. 5. Now f(5) > 0, so we choose left sub-interval [1,5] (as any value in right sub-interval [5,9] would give more positive value of 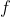 ).
).
In second iteration, we choose mid point of [1,5] i.e. 3, but again f(3) > 0, so we again choose left sub-interval [1,3].
In third iteration, we choose mid point of [1,3] i.e. 2, now f(2) = 0
So we found root in 3 iterations. So answer is option (B).