Kruskal's algorithm is an algorithm that finds a minimum spanning tree for a connected weighted graph. It finds a safe edge to add to the growing forest by finding, of all the edges that connects any two trees in the forest, an edge $(u,v)$ of least weight. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
The given graph is
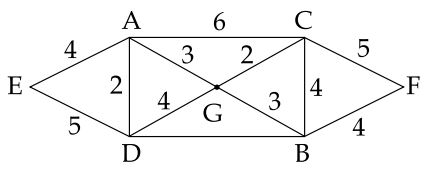
We can see that $DB's$ weight is not given.
We know that, for any weighted graph, if the weight of an certain edge isn't given, then the weight'll be $1$(default)
| Edge No. |
Vertex Pair |
Edge Weight |
| E1 |
(B,D) |
1 |
| E2 |
(G,C) |
2 |
| E3 |
(A,D) |
2 |
| E4 |
(B,G) |
3 |
| E5 |
(A,G) |
3 |
| E6 |
(A,E) |
4 |
| E7 |
(D,G) |
4 |
| E8 |
(B,C) |
4 |
| E9 |
(B,F) |
4 |
| E10 |
(D,E) |
5 |
| E11 |
(C,F) |
5 |
| E12 |
(A,C) |
6 |
Graph
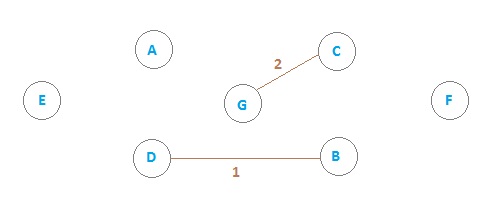
Add edge E1

Add edge E2
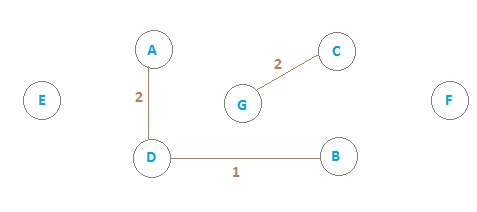
Add edge E3
Add edge E4

Edge E5 will not counted, as it'll create cycle.
Add edge E6
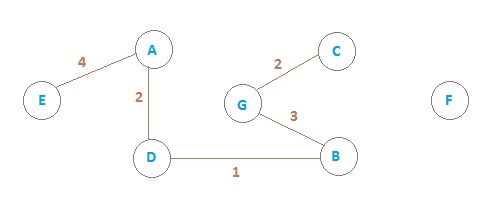
Edge E7,E8 will not counted, as it'll create a cycle.
Add edge E9
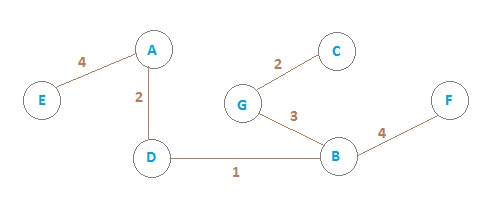
Edge E10, E11, E12 will not connected, they'll make a cycle.
∴ $\color{green}{\text{Total Cost}}= 1+2+2+3+4+4$
$\qquad\qquad = \color{gold}{16}$
$\color{violet}{\text{The List of the edges of the tree in the order in which they are choosen is}}$ $\color{maroon}{\text{BD, GC, AD, BG, AE, BF}}$