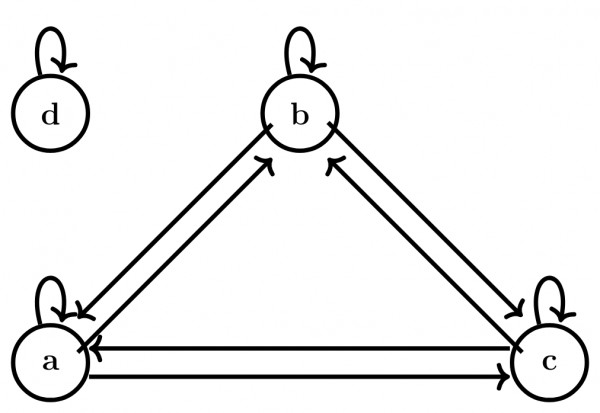
a. For Calculating Ordered Pairs Just multiply the partition with itself.
$ \{a,b,c\} * \{a,b,c\} = \{ (a,a),(a,b),(a,c),(b.a),(b,b),(b,c),(c,a),(c,b),(c,c)\}$
$ \{d\}*\{d\} = \{(d,d)\}$
$\therefore$ The ordered pairs of the equivalence relations are $= \{ (a,a),(a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c),(d,d) \}$
b. For each ordered pair $(a,b)$ in the equivalence relation just make a directed edge from a towards $b$.
c. Suppose we have two partitions of a set $S:P_1={A_1,A_2,A_3...}\ and\ P_2={B_1,B_2,B_3...}$
We say that $P_1$ is a refinement of $P_2$ if every $A_i$ is a subset of some $B_j$ . Or We can say that $P_1$ refines $P_2$
Additional Note :-
First read definition of refinement given above then relate it to this example.
Refinement means refining/filtering elements.
Suppose like we have { water, ice, sugar, rasna }
now someone told you to make sugarfree rasna so you keep sugar aside like {{water,ice,rasna},{sugar}}
now someone told you to not to put ice in rasna so you do keep ice aside like {{water,rasna,sugar},{ice}}
i.e. {{water,ice,rasna},{sugar}} and {{water,rasna,sugar},{ice}} are refined versions of { water, ice, sugar, rasna } in one you have refined sugar and in other you refined ice.
now someone told you to make sugarfree rasna and also not add ice then you do like {{water,rasna},{ice,sugar}}.
Now this is another refined version of { water, ice, sugar, rasna } and not refined version of {{water,ice,rasna},{sugar}} or {{water,rasna,sugar},{ice}} . why ?
because {ice,sugar} is not a subset of {water,ice,rasna} or {water,rasna,sugar} but it is a subset of { water, ice, sugar, rasna }