Let us first draw the cache with the configuration given in the question
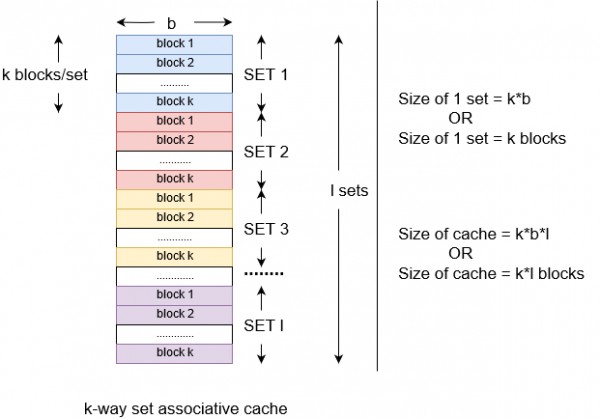
In question, we are given a loop that executes for $100$ times and the size of loop is $n*b$ or we can say $n$ blocks.
i.e. The loop requires $n$ blocks of data in each iteration.
Let us now execute the loop,
Iteration 1
First the CPU checks whether the data i.e. $n$ blocks that the loop requires to execute in the first iteration is present in the cache or not.
In worst case it may happen that none of the $n$ blocks that we require are present in the cache memory.
So we go to main memory and select those $n$ blocks and also bring them in cache memory so that iteration $1$ could be executed successfully.
Given : $n= k*m$ and in worst case $m=l\ (\because 1 \leq m \leq l)$
i.e. in worst case $n = k*l$ .......$eq (i)$
i.e. number of blocks that we need to bring into cache memory from main memory for iteration $1$ at max.
$=n$ blocks
$=k*l$ blocks
$=$ size of cache. (from diagram)
Hence, we can say that in iteration $1$ all the data that we require = The size of cache memory (at max)
and after bringing the data in cache, the iteration $1$ of loop is executed successfully.
$\therefore$ iteration $1$ was a $MISS$ case since we did not found the data that we were looking for in the cache memory.
How many misses and block accesses were there ?
We need to bring $k*l$ blocks into the cache.(From $eq (i)$)
Also, the cache is set associative so we could bring $k$ blocks whenever a miss is encountered for a block.
Eg :-
if block $1$ of set $1$ is missing we could bring $k$ blocks of set $1$ in cache.
if block $1$ of set $2$ is missing we could bring $k$ blocks of set $2$ in cache.
..........
if block $1$ of set $l$ is missing we could bring $k$ blocks of set $l$ in cache.
We can do this because initially the whole cache is empty.
From this we can say that there were $l$ block misses and we brought $k*l$ blocks or $n$ blocks ( From $eq(i)$ ) into the cache memory.
Iteration 2
Now the CPU again checks whether the data i.e. $n$ blocks that the loop requires to execute in the second iteration is present in the cache or not.
Now in this case the loop will require the same set of data that it required in iteration $1$ ( since a for loop is used to execute same set of instructions again and again)
And we know that the data is present in cache since we have already loaded them in iteration $1$.
$\therefore$ iteration $2$ would be a $HIT$ case since we found the data that we were looking for in the cache memory.
How many misses and block accesses were there ?
As already explained above there are no misses since data blocks that we require are already present in cache.
This iteration also needed $l*k$ blocks of data i.e. $n$ blocks ( From $eq(i)$ )
Similarly, the remaining $98$ iterations of the loop would also be counted as $HIT$ cases and each one of them require $l*k$ blocks of data i.e. $n$ blocks ( From $eq(i)$ )
$\therefore \ Miss\ Ratio\ =\frac{Miss\ cases}{Total\ blocks\ access\ required}= \frac{l}{l*k+l*k+l*k....._{100\ times}} = \frac{1}{100k} $
$\therefore \ Hit\ Ratio\ =1 - \ Miss\ ratio\ = 1 - \frac{1}{100k}= \frac{100k-1}{100k} = 1 - \frac{1}{100k} $
Now in worst case $k=1b$ i.e. each set has only $1$ block.
$\therefore \ Hit\ Ratio\ = 1 - \frac{1}{100b} $