The question is indirectly asking for static-$1$ hazard in the circuit - that is output becoming $0$ momentarily when it is supposed to be $1.$
$\text{Static 1 Hazard:}$ Output going to $0$ when it should remain $1$
- Happens in a $2$ level $\text{SOP}$ implementation.
- Suppose only one $\text{AND}$ gate (minterm) is $1$ in an $\text{SOP}$ implementation.
- A variable in that minterm changes causing the output of that $\text{AND}$ gate to become $0$ and another AND gate to be $1.$
- Depending on the propagation delay of the gates, the output can momentarily become $0$ before finalizing on $1.$ For example, consider $f = a’b’ + ac$ and initially $a = 0,b = 0, c = 1,$ so that output is $1.$ Now, if $a$ changes to $1,$ again output should be $1$ due to $ac$ term. But if $a’b’$ turns to $0$ before $ac$ turns to $1,$ output can be momentarily $0$ causing a static- $1$ hazard.
- Can be detected in a K-map if there are any adjacent $1$'s not covered by an implicant. i.e., to avoid static hazard, all adjacent $1$’s in a K-map must be covered by some implicant. In the below K-map, the implicant shown in green ensures no static-$1$ hazard.

Here $f(w,x,y,z) = \sum (5,7,11,12,13,15)$
So, $K$-map will be
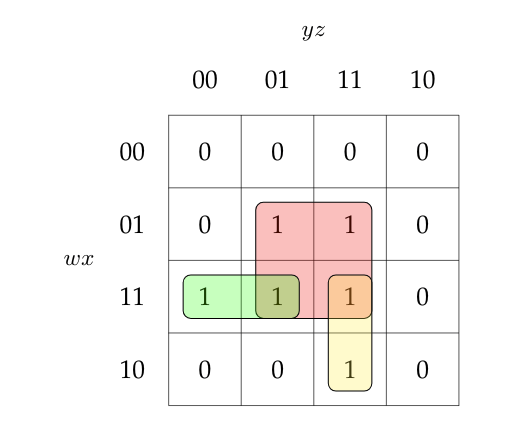
So, its minimized sum of product expression will be $xz + wxy' + wyz$. Since all the minterms are overlapping, there is no chance of static hazard here.
Now, let's consider the options one by one:
A. $\overline{w}xz,wx\overline{y},x\overline{y}z,xyz,wyz$
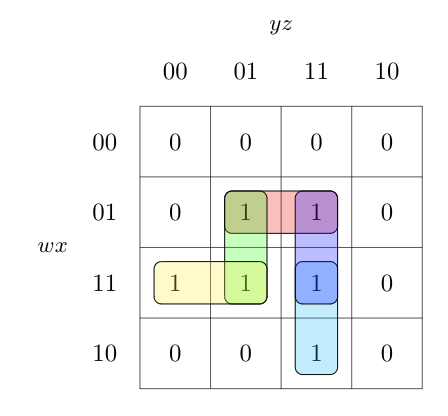
Chance of static hazard.
Here, when $y$ changes from $0$ to $1$, the gate for $wyz$ should give $1$ (from earlier $0,$ assuming $w=z=1$) and that of $xy'z$ should give $0$ (from earlier $1$). But there is a possibility of circuit giving $0$ (static $1$ hazard) momentarily due to gate delays ($xy'z$ coming first and $wyz$ coming later). In order to avoid this, we must add a gate with $wxz$ also which ensure that all adjacent blocks in $K$-map are overlapped or a single variable change cannot momentarily change the circuit output.
B. $wxy, \overline{w}xz,wyz$
This is not correct as $wxy$ is not a minterm for the given function
C. $wx\overline{y} \overline{z}, xz, w\overline{x}yz$
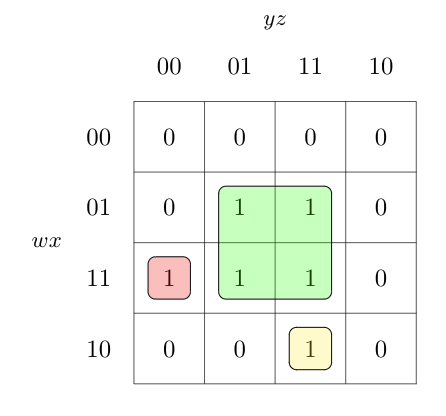
Here, also static-$1$ hazard is possible as the middle $4$ pairs are separated by $1$ bit difference to both $wxy'z'$ as well as $wx'yz$. Could have been avoided by using $wxy'$ instead of $wxy'z'$ and $wyz$ instead of $wx'yz$ which will ensure that all neighboring blocks are overlapped.
D. $wx\overline{y}, wyz, wxz, \overline{w}xz, x\overline{y}z, xyz$

These minterms cover all the minterms of $f$ and also, all the neighboring $1$'s are overlapped by minterms. So, no chance of hazard here, and hence is the required answer.
Correct Answer: D.