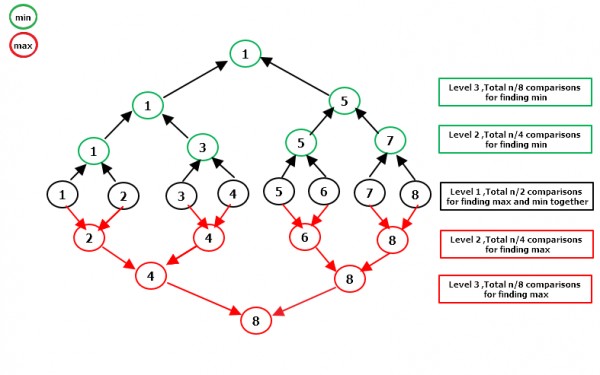
NOTE: At level 1 in $\frac{n}{2}$ comparisons we are finding Both MINIMUM as well as MAXIMUM for level 2.
Let's see for minimum,
At level 1 :$\frac{n}{2}$ comparisons
At level 2 : $\frac{n}{2^2}$ comparisons
At level 3 : $\frac{n}{2^3}$ comparisons
so on....
At level logn : $\frac{n}{2^{logn}}$ comparisons
So, Total number of comparisons will be
$\frac{n}{2}$ + $\frac{n}{2^2}$ + $\frac{n}{2^3}$ + .....+ $\frac{n}{2^{logn}}$
$\Rightarrow$ n ($\frac{1}{2}$ + $\frac{1}{2^2}$ + $\frac{1}{2^3}$ + .....+ $\frac{1}{2^{logn}}$ ) [apply Sum of G.P]
$\Rightarrow$ $n\frac{1}{2}(\frac{1-(\frac{1}{2})^{logn}}{1-\frac{1}{2}})$
$\Rightarrow$ $n\frac{1}{2}(\frac{1-(2)^{-logn}}{\frac{1}{2}})$
$\Rightarrow$ $n(1-\frac{1}{n})$
$\Rightarrow$ $n-1$
So,total comparisons required to find minimum of n element is n-1 comparisons.
similarly for Max n-1 comparisons required.
So total comparisons for both min and max will be
$2(n-1) - \frac{n}{2}$ $\Rightarrow$ $\frac{3n}{2}-2$
[ $\frac{n}{2}$ is reduced because at Level 1 we have taken $\frac{n}{2}$ for both while min and max calculation ]
coming to question n = 100,
total comparisons $\Rightarrow$ $\frac{3 * 100}{2}-2 = 148$