1) The definition of a lattice is that for any two elements, they must have a join and a meet. The proof is by contradiction. Assume that a finite lattice is not bounded. This means that there is no single element that is a maximum or that there is no single element that is a minimum. Since the lattice is finite, however, there are a finite number of maxima and of minima, which can be identified by starting from all pairs of elements and following their joins or meets, respectively, until the join or meet is identical to one of the current pair. The element obtained is one of the maxima or one of the minima, respectively. By the assumption, either or both of the sets of maxima and minima have cardinality greater than one. Therefore, there exist two elements in the finite lattice that have no join and/or have no meet. This contradicts the definition of a lattice, which requires any two elements to have a join and a meet.
2)A complemented lattice is a bounded lattice
3) A bounded and complemented lattice may not be distributive is True
if a lattice is ISOMORPHIC TO L1* OR L2* then it will not be distributive
see Image below
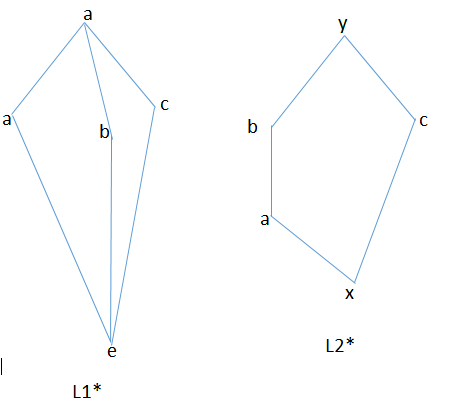
If Lattice contains a sub lattice which is isomorphic to one of these two then we can say Lattice is not distributive and otherwise it is distributive