expression trees post-order gives us postfix notation.
expression trees pre-order gives us prefix notation.
if 7 7 1 ↑ 7 1 * / + 7 − is post order, then - + 7 / ↑ 7 1 * 7 1 7 is it's pre order.
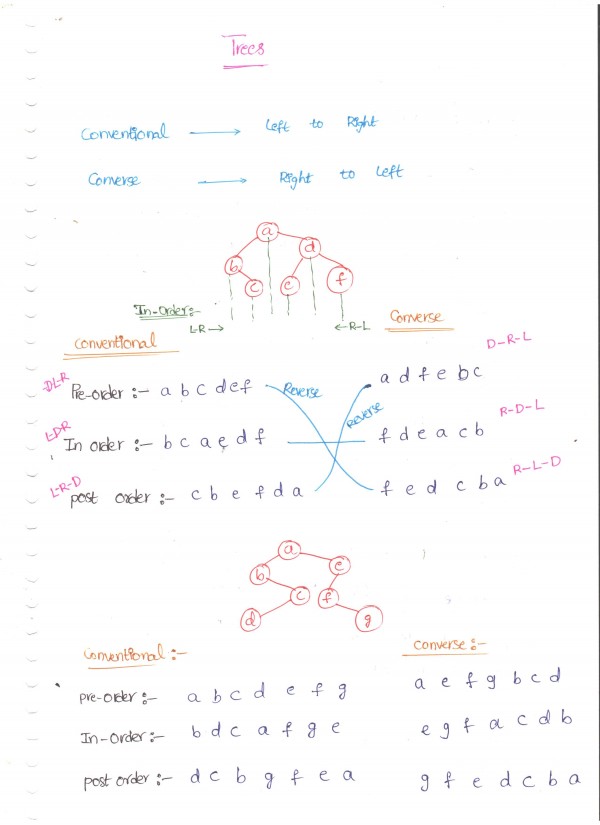
last level order strategy on a Tree ( not standard as per given rule ) ====> print Right , Print Left , Print DATA.
What is our well known strategy of preorder ==> Print Data, Print Left, Print Right
this is exactly reverse of the last level strategy post-order !
Post-order of last level strategy on the Tree = Reverse ( Well known Pre-order on the Tree )
= Reverse ( - + 7 / ↑ 7 1 * 7 1 7 ) = 7 1 7 * 1 7 ↑ / 7 + -