- $Q_{3N} = D_3 \Rightarrow Q_{3N} = Q_2$
- $Q_{2N} = D_2 \Rightarrow Q_{2N} = Q_1$
- $Q_{1N} = D_1 \Rightarrow Q_{1N} = Q_3 \oplus Q_2$
$$ \begin{array}{|ccc|ccc|} \hline \textbf{$Q_1$} & \textbf {$Q_2$} &\textbf {$Q_3$} & \textbf {$Q_{1N}$} & \textbf{$Q_{2N}$} & \textbf{$Q_{3N}$}\\\hline0&0&0&0&0&0 \\\hline 0&0&1&1 &0 &0\\\hline 0&1&0&1&0&1\\\hline0&1&1&0&0&1 \\\hline1&0&0&0&1&0 \\\hline 1&0&1&1 &1 &0\\\hline 1&1&0&1&1&1\\\hline1&1&1&0&1&1 \\\hline \end{array}$$Given that the initial state $=S_4 = 100.$
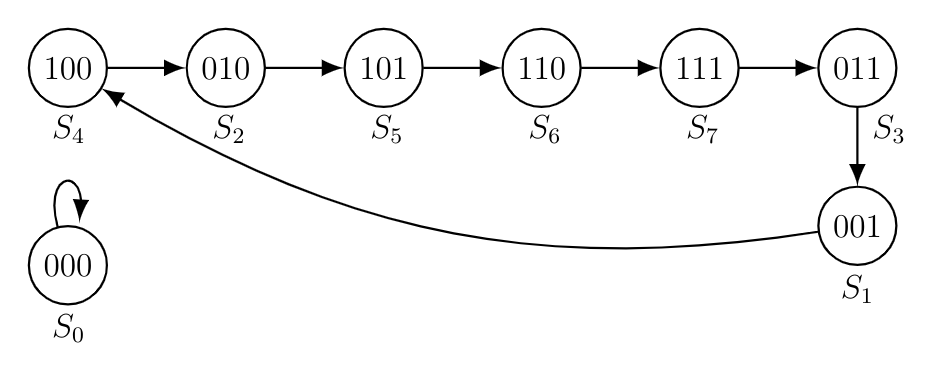
Unreachable state is $S_0$
So, set of states which are not reachable $= \{S_{0}\}$