GATE2001-11-b

Question

A sequential circuit takes an input stream of 0's and 1's and produces an output stream of 0's and 1's. Initially it replicates the input on its output until two consecutive 0's are encountered on the input. From then onward, it produces an output stream, which is the bit-wise complement of input stream until it encounters two consecutive 1's, whereupon the process repeats. An example input and output stream is shown below.$$\begin{array}{ll|ll}\hline \textbf{The input stream:} & 101100\mid 01001011 & 0\mid 11 \\\hline  \textbf{The desired output:} & 101100\mid 10110100& 0\mid 11  \\\hline \end{array}$$J-K master-slave flip-flops are to be used to design the circuit.

Give the minimized sum-of-product expression for J and K inputs of one of its state flip-flops

Answer 1

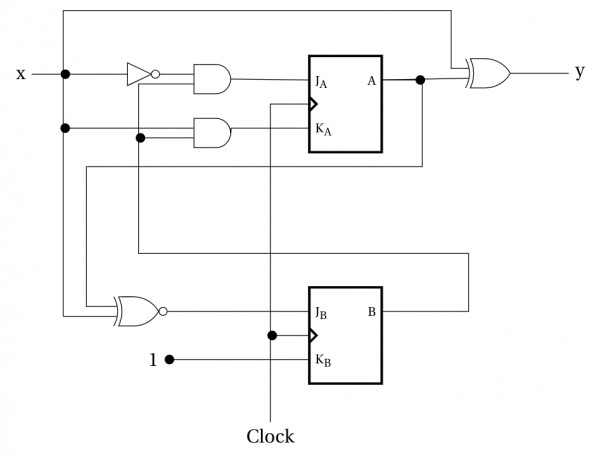
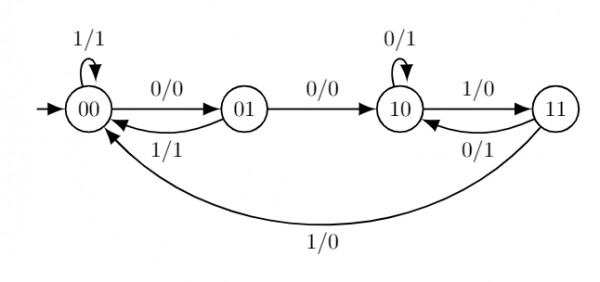
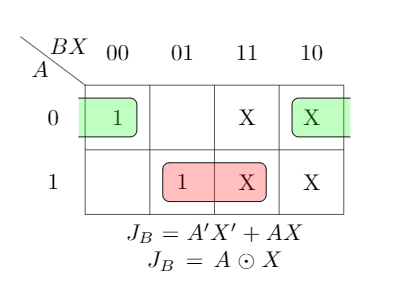We can design a Mealy Machine as per the requirement given in the question. 

From which we will get state table, and we can design sequential circuit using any Flip-flop from the state table (with the help of excitation table) :

As we get $4$ states (renaming state component to binary states), we need two FFs to implement it.

Let $A$ and $B$ be present states, $x$ be the input and $y$ be the output.$$\small \begin{array}{c|c|c|c|cc|cc|}
\text{Present State}&\text{Input}&\text{Next State}&\text{Output}&\rlap{\text{FF}}&&\rlap{\text{FF}}\\
&&&&\rlap{\text{inputs}}&&\rlap{\text{inputs}}\\
\hline
AB&X&A'B'&Y&J_A&K_A&J_B&K_B\\\hline
00&0&01&0&0&X&1&X\\
00&1&00&1&0&X&0&X\\
01&0&10&0&1&X&X&1\\
01&1&00&1&0&X&X&1\\
10&0&10&1&X&0&0&X\\
10&1&11&0&X&0&1&X\\
11&0&10&1&X&0&X&1\\
11&1&00&0&X&1&X&1\\
\end{array}$$ \begin{array}{cc|cc} Q_t&Q_{t+1}&J&K\\\hline 0&0&0&X\\0&1&1&X\\1&0&X&1\\1&1&X&0\end{array}

 

Comments

In the question they mention " J-K master-slave flip-flops are to be used to design the circuit. "

But you did with Melay and Moore

---

@shaik .. it is state machine to sequential logic circuit

---

nice idea praveen sir

---

Sir how to draw this mealy machine

---

as you did in TOC.

---

Sir how the solution will change if we had to do it using norml JK Flip Flop

---

you can refer my answer, for normal J-K flipflop

But with master slave J-K flipflop i don't know.

Moreover no need to call me as sir, you can call me with my name

---

Shaik Masthan  Can u please write your solution in detailed manner like this answer.

---

there is no need of it, For avoiding confusion, i removed my answer !

---

 Shaik Masthan Please add your answer. I want to learn to design circuit without Master Slave Filp Flop also

---

Actually i made the wrong statement, sorry for that !

there is no specific representation for Master-slave FF, in this answer the A flipflop and B flipflops are Master slave Flipflop's only ! ( the internal circuit is different for normal and master-slave, but o/p is same. )

Then Why my answer is not Matching ?

without state diagram, i tried and got with 3-FF, it is not minimized !

---

Just one doubt how could you replace q0 with 00.. why can't we replace it with 11(or any other combination).. can you please help me with this @Shaik Masthan @Praveen Saini

---

normally in the state diagram, the states are represented the o/p of FF's only.

By taking the initial state as 00, we form that entire sequence !

---

normally in the state diagram, the states are represented the o/p of FF's only.

Here what is the output of FF, we don't know about it right ??

 By taking the initial state as 00, we form that entire sequence !

I agree we generally take 00 as initial state unless it is specified to take any other value, but how will the second state be 01 ? :(

---

How are the inputs of the flip flop B obtained here in the table?

---

@sambhrant using excitation table of FF, where present state and next state is given.