Some important things, we should know
- ${\color{Red} {\cos 0 = 1,\cos \pi = -1,\cos 2\pi = 1,\dots}}$
- ${\color{Blue}{ \text{In general}\: \cos n\pi = (-1)^{n}\: \text{where}\: n=0,1,2,\dots}}$
- ${\color{Magenta} {\sin 0 = 0,\sin \pi = 0,\sin 2\pi = 0,\dots}}$
- ${\color{Green} {\text{In general}\: \sin n\pi = 0\: \text{where}\: n=0,1,2,\dots}}$
- ${\color{Orange} {\sin(\pi-x)=\sin x,\sin (2\pi-x)=-\sin x,\sin(3\pi-x)=\sin x}}$
- ${\color{Teal} {\text{In general}\: \sin (n\pi-x)=(-1)^{n+1}\sin x\: \text{ where} \: n=0,1,2,\dots}}$
- ${\color{Orchid} {\cos(\pi-x)=-\cos x,\cos (2\pi-x)=\cos x,\cos (3\pi-x)=-\cos x}}$
- ${\color{purple} {\text{ In general}\: \cos (n\pi-x)=(-1)^{n}\cos x \: \text{where}\: n=0,1,2,\dots}}$
$f(x)=\sin x$

$f(x)=\cos x$
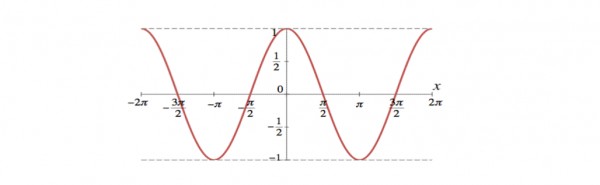
Visualization:

_________________________________________________________________
Let $I = \displaystyle{}\int_{0}^{2\pi} \mid x \sin x \mid {\mathrm{d} x} = k\pi\rightarrow(1)$
Now, we should break the limits and open the 'modulus function'.
$I = \displaystyle{}\int_{0}^{\pi} x \sin x \: {\mathrm{d} x} - \displaystyle{}\int_{\pi}^{2\pi} x \sin x\: {\mathrm{d} x}$
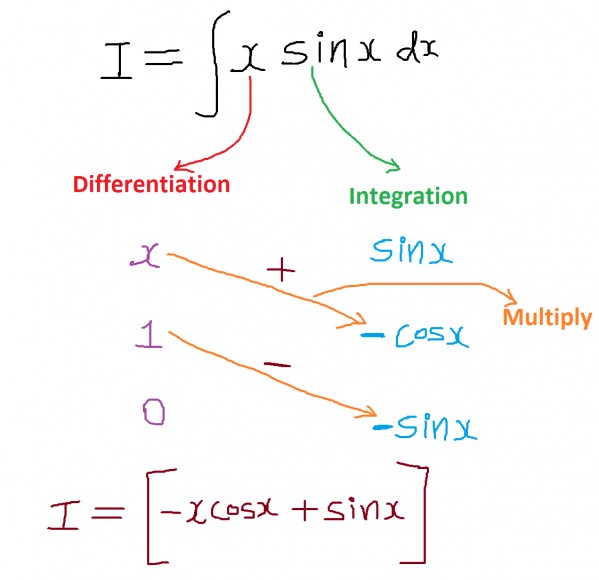
Now, $I = \left[-x \cos x + \sin x \right]_{0}^{\pi} - \left[-x \cos x + \sin x \right]_{\pi}^{2\pi}$
$\implies I = \left[ \left(- \pi \cos \pi + \sin \pi \right) - \left(-0 \cos 0 + \sin 0 \right) \right] - \left[ \left(- 2\pi \cos 2\pi + \sin 2\pi \right) - \left(- \pi \cos \pi + \sin \pi \right) \right]$
$\implies I = \left[ \left(- \pi (-1) + 0 \right) - \left( 0 + 0 \right) \right] - \left[ \left(- 2\pi (1) + 0 \right) - \left(- \pi (-1) + 0 \right) \right]$
$\implies I = \pi + 2\pi + \pi $
$\implies I = 4\pi = k\pi\implies k = 4$
So, the correct answer is $k = 4.$