Here, Independent sets, $S_1 = \{a,d\}, S_2 = \{b,e\}, S_3 = \{c,f\}$
Therefore, vertices of $S_1$ has no connection between each other [∵ $a$ & $d$ are not connected by an edge]
$ S_1 ⇒ $put ${\color{red}{RED}}$

Vertices of $S_2$ has no connection between each other [∵ $b$ & $e$ are not connected by an edge]
$ S_2 ⇒ $put ${\color{GREEN}{GREEN}}$
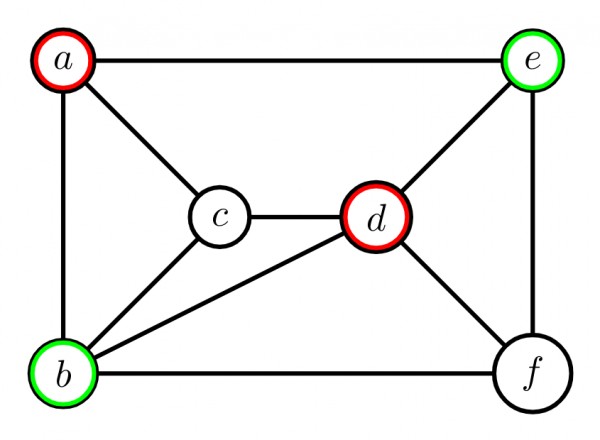
Vertices of $S_3$ has no connection between each other [∵ $c$ & $f$ are not connected by an edge]
$ S_3 ⇒ $put ${\color{BLUE}{BLUE}}$
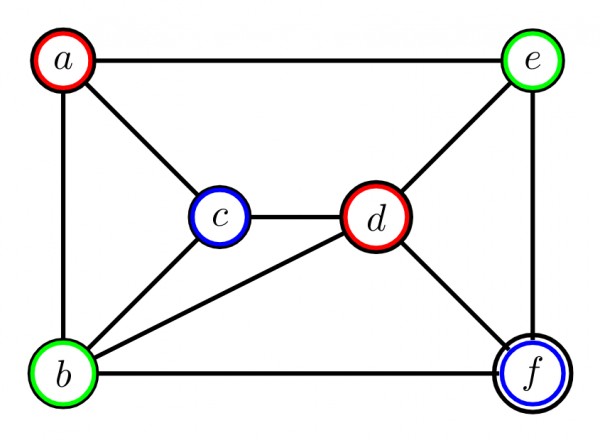
∴ These graph has chromatic number as $3$.
Explanation: Why solving by independent sets?
Independent set means a set containing vertices & each & every vertex of this set is independent to each other i.e. if there are $3$ vertices in an independent set, then each vertex of this set does not connected to other vertex of this set by an edge.
Suppose, there are two independent sets $(S_1$ & $S_2)$. Then any vertex of $S_1$ has connection(share an edge) to any vertex of set $S_2$.
∵ $S_1,S_2, S_3$ are different independent sets & they share some connection between them, we put different colours to different sets.
$S_1$ share connections to $S_2$ & $S_3$
∴ Put ${\color{RED}{RED}}$ to $S_1$, not $S_2$ & $S_3$
Similarly, $S_2$ share connections to $S_1$ & $S_3$
∴ Put ${\color{GREEN}{GREEN}}$ to $S_2$, not $S_1$ & $S_3$
$S_3$ share connections to $S_1$ & $S_2$
∴ Put ${\color{BLUE}{BLUE}}$ to $S_3$, not $S_1$ & $S_2$
The advantage of following this method is when we have a complicated graph then we do not need to continuously see whether any vertex is adjacent to each other when we colour any vertex.