GATE CSE 2018 | Question: 31

Question

Assume that multiplying a matrix $G_1$ of dimension $ p \times q$ with another matrix $G_2$ of dimension $q \times r$ requires $pqr$ scalar multiplications. Computing the product of $n$ matrices $G_1G_2G_3 \dots G_n$ can be done by parenthesizing in different ways. Define $G_i G_{i+1}$ as an explicitly computed pair for a given paranthesization if they are directly multiplied. For example, in the matrix multiplication chain $G_1G_2G_3G_4G_5G_6$ using parenthesization $(G_1(G_2G_3))(G_4(G_5G_6)), G_2G_3$ and $G_5G_6$ are only explicitly computed pairs.

Consider a matrix multiplication chain $F_1F_2F_3F_4F_5$, where matrices $F_1, F_2, F_3, F_4$ and $F_5$ are of dimensions $ 2 \times 25, 25 \times 3, 3 \times 16, 16 \times 1 $ and $ 1 \times 1000$, respectively. In the parenthesization of $F_1F_2F_3F_4F_5$ that minimizes the total number of scalar multiplications, the explicitly computed pairs is/are

• A. $F_1F_2$ and $F_3F_4$ only
• B. $F_2F_3$ only
• C. $F_3F_4$ only
• D. $F_1F_2$ and $F_4F_5$ only

Comments

Option D has typo error

---

i am confusing addtion of sacalar multiplication if multiply like this ((F1.F2)(F3.F4)).

 (# of Multiplication  F1.F2=150) and (# of Multiplication  F3.F4=48)

after that result of F1.F2 multiply with result of F3.F4 so # of multiplication is 6

Now total multiplication is 150+48+6

if i am wrong please correct me.

---

Saurabh Pal

Already explained in the question itself !

Answer 1

If we multiply anything with $F_{5}$ we will get much greater multiplication cost because $F_{5}$ is $1*1000$ matrix so $1000$ will play vital role in cost. So we will multiply $F_{5}$ at very last step.

So, here is the sequence giving minimal cost:

$(F_{1}(F_{2}(F_{3}F_{4})))(F_{5}) =  48 + 75 + 50 + 2000 =  2173$

Explicitly computed pairs is $(F_{3} F_{4} )$

Correct Answer: $C$

Comments

What is the meaning of explicit pairs ?

---

Explicit pairs mean two matrices which are being multiplied directly with each other.

For example, take $M_{1}( M_{2}( M_{3}M_{4}))$.

Here, $M_{3}, M_{4}$ are multiplied to each other first. Their product is then multiplied with $M_{2}$. And the next resultant product is then multiplied with $M_{1}$.

$M_{3}M_{4}$ is an explicit pair here.

---

Refer for the clear explanation:- (160) GATE CS 2018 | Q31:Assume that multiplying a matrix G1 of dimension p×q with another matrix G2 of - YouTube

Answer 2

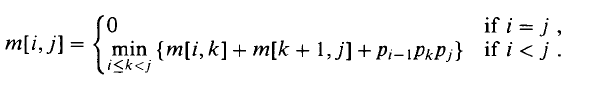
$\large I^{st}\space part$

$M[1,2] = M[1,1] + M[2,2] + P_0P_1P_2 = 2\times 25\times 3= 150 $

$M[2,3] = P_1P_2P_3 = 25\times 3\times16=1200$

$M[3,4] = P_2P_3P_4 = 3\times 16\times1=48$

$M[4,5] = P_3P_4P_5 = 16\times 1\times1000=16000$

 

$\large II^{nd}\space part$

In $M[1,3] $ $M[1,2]$ is minimum so

$M[1,3] = M[1,2] + M[3,3] + P_0P_2P_3 = 150 + 2\times 3\times 16=243$

so minimum is $M[3,4]$ so

$M[2,4] = M[2,2] + M[3,4] + P_1P_2P_4 = 48 + 25\times3\times1 = 123 $

now compute further and $M[2,4] $ is minimum so

in $M[3,5]$ $M[3,4]$ is already minimum so

$M[3,5] = M[3,4] + M[5,5] + P_2P_4P_5 = 48 + 3\times 1\times 1000 = 3048 $

 

$\large III^{rd}\space part$

In previous part $M[2,4]$ is minimum

$M[1,4] = M[1,1] + M[2,4] + P_0P_1P_4 = 123 + 2\times 25\times 1=173 $

$M[2,4]$ is minimum so

$M[2,5] = M[2,4] + M[5,5] + P_1P_4P_5 = 123 + 25\times 1\times 1000= 25123$

 

$\large IV^{th}\space part$

$M[1,4]$ is minimum in previous part so

$M[1,5] = M[1,4] + M[5,5] + P_0P_4P_5 = 173 +2\times 1\times 1000 = 2173$

 

Now we can see-

$(F_1F_2F_3F_4F_5) \implies ((F_1F_2F_3F_4)F_5) \implies ((F_1(F_2F_3F_4))F_5) \implies((F_1(F_2(F_3F_4)))F_5)  $

 

So Option C is right one

Comments

Thank you. Just a tiny correction, M[1, 3] should be 246, not 243 though final answer is correct.

---

Thanks, bro for your solution, it seems like a more meaningful way than trying all parenthesizes and a

more systematic way

---

Thx for the solution . It means a lot .

Answer 3

May be this works :

Comments

Thx for the solution . It means a lot .

Answer 4

Read comment of @akash.dinkar12 under @Digvijay Pandey 's answer and refer this 👇

Comments

This is the way smart people works. Thx for it bro .

---

thats an easy way