Consider the following undirected graph with some edge costs missing.
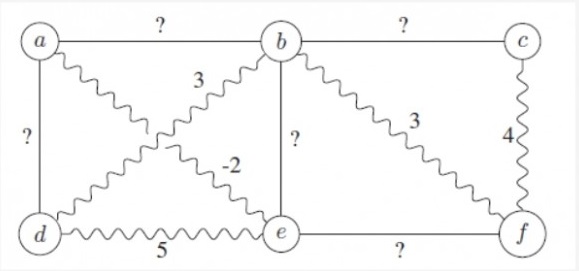
Suppose the wavy edges form a Minimum Cost Spanning Tree for $G$. Then, which of the following inequalities NEED NOT hold?
- $cost(a,b)\geq 6$.
- $cost(b,e)\geq 5$.
- $cost(e,f)\geq 5$.
- $cost(a,d)\geq 4$.
- $cost(b,c)\geq 4$.
Please someone solve and explain :)