The result to be utilised here is that K3,3(complete bipartite graph with 3 vertices in each partition) and k5(5 vertex complete graph) are simplest non-planer graphs.
KURATOWSKI THEOREM: ANY GRAPH WHICH CONTAINS SUBGRAPHS HOMEOMORPHIC TO K3,3 OR K5 ARE NON-PLANER (NOTE THAT IT IS AN IF AND ONLY IF CONDITION).
A graph is non-planar iff we can turn it into K3,3 or K5 by:
-
Removing edges and vertices. (Making a subgraph.)
-
Collapsing degree-two vertices into a single edge.
-
Applying an isomorphism to turn it into K3,3 or K5.
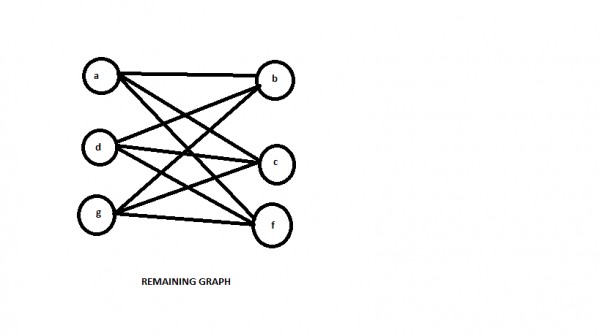
In the above graph ,
- remove vertex e
- put {a,d,g} in one partition
- put {b,c,f} in other partition
- remove edges between {a,d},{a,g},{g,d},{b,c},{b,f},{f,c}