This statement is not true, because the number of bad edges in a directed graph (contains cycles) is varies with different starting vertices and doesn’t always minimizes the bad edges. Selecting different starting points, the topological ordering will give different sequences and the number of bad edges cannot be guaranteed to be the least or same.
The bad side or edge of a graph is nothing but the Back Edge. In the statement minimizing the number of bad edges that are inconsistent with the linear order meaning that the TOPOLOGIAL-SORT(G) will maximize the number of tree edges.
Let us consider the following example.
Consider the graph G consisting of vertices a, b, c and d. let the edges be (a, b), (b, c), (a, c), and (c, a)
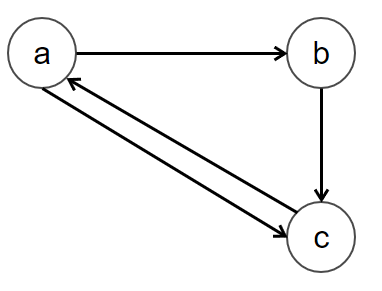
Suppose, if we start the DFS of TOPOLOGICAL-SORT(G) at vertex ‘a’ and assume that each adjacency list is ordered alphabetically. then Topological order: a, b, c
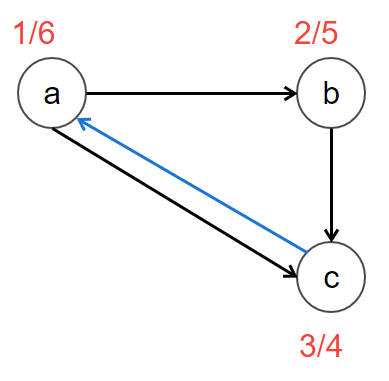
In this case the bad edge are only one i.e. c->a
Now let’s take same graph and the DFS of TOPOLOGICAL-SORT(G) at vertex ‘b’. then the topological order become b, c, a.
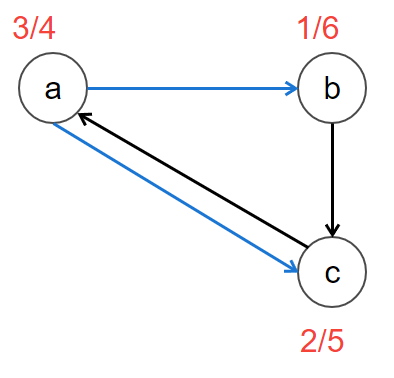
In this case the bad edge are now two i.e. a->c && a->b
Thus the TOPOLOGICAL-SORT doesn’t always minimizes the number of bad edges.