In sum of terms, any term is an implicant because it implies the function. So, $xz$ is an implicant and hence C is the answer. Still, lets see the other options.
If no minimization is possible for an implicant (by removing any variable) it becomes a prime implicant.
If a prime implicant is present in any possible expression for a function, it is called an essential prime implicant. (For example in K-map we might be able to choose among several prime implicants but for essential prime implicants there won't be a choice).
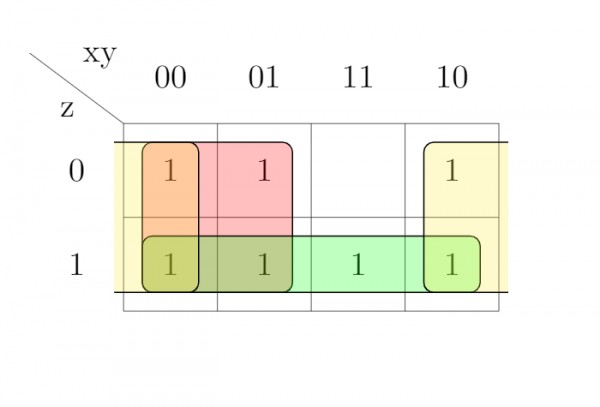
So, $f = x' + y'x + xz$
$= y' + x' + z$ (could be also derived using algebraic rules as in http://www.ee.surrey.ac.uk/Projects/Labview/boolalgebra/ )
So, the prime implicants are $x', y'$ and $z$. Being single variable ones and with no common variables, all must be essential also.
Choice a) False - $y'$ is a prime implicant and hence, $y'x$ is just an implicant but not prime.
Choice b) False - $xz$ is not a minterm. A minterm must include all variables. So, $xyz$ is a minterm so, is $xy'z$, but not $xz$.
Choice d) False - $y'$ is a prime implicant not $y$.