To make this partial order a total order, we need the relation to hold for every two element of the partial order. Currently between any $a_i$ and $a_j,$ there is no relation. So, for every $a_i, a_j,$ we have to add either $(a_i, a_j)$ or $(a_j, a_i)$ in total order. So, this translates to giving an ordering for $n$ elements between $x$ and $y,$ which can be done in $n!$ ways. So, answer is (a).
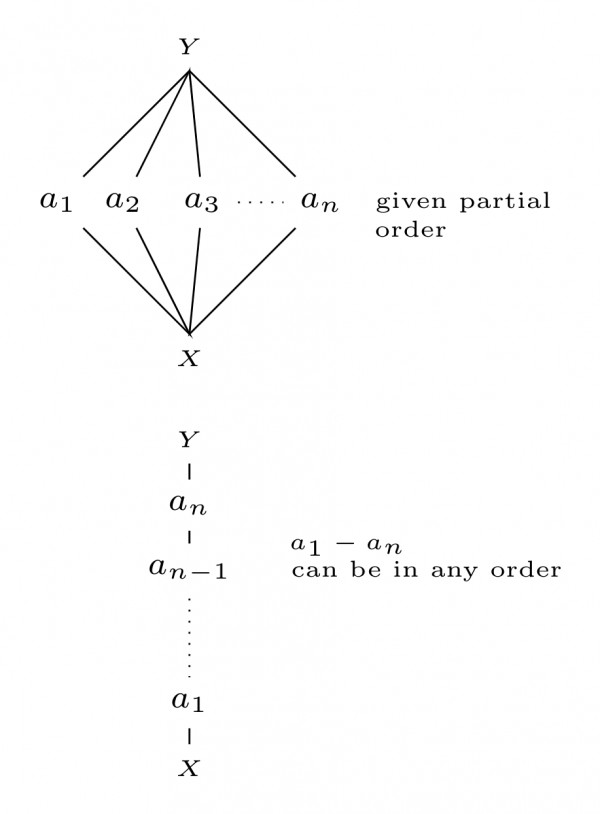
The bottom figure is for a total order. We can permute the $a_i$ from $i = 1$ to $n,$ and each permutation will also be a total order containing the given partial order.