In general for RMO we calculate like :
Let A[LR.....UR][Lc.....Uc] be a 2D array
Address of A[i][j]= Base + Size of each element { (no. of rows fully covered before reaching row i x no. of columns in each row) + no. of elements covered in the current row i}
no. of rows fully covered = (i-LR)
no. of columns in each row= (Uc-Lc+1)
But here the case is a bit different. The elements are arranged in lower triangular matrix form like this:
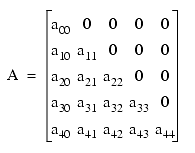
The rows are not fully covered.
The 1st row has 1 element.
The 2nd row has 2 elements. The 3rd has 3 elements and so on.
So kth row will have k elements.
No. of elements covered upto k rows is 1+2+3....k = k(k+1)/2.
We need to find address of A[i][j]. To reach this row no. i we have to cover previous (i-LR) rows.
So, no. of elements covered in (i-LR) rows is ((i-LR)* (i-LR+1))/2 rows
Now we are at row no. i.
No. of elements covered in this row no. i is (j-Lc) elements.
Address of A[i][j]= Base + size( ((i-LR)* (i-LR+1))/2 + (j-Lc))
Address of A[66][50] = 1000 + 1 ( (66-40)*(66-40+1)/2 + (50-40) ) = 1000 + (26*27/2 + 10 ) = 1000 + (351+10) =1361
------------------------------------------------------------------------------------------------------
We need to find address of A[66][50]. To reach this row no. 66 we have to cover (66-40)= 26 rows.
So, no. of elements covered in 26 rows = 26*(26+1)/2 = 351
Now we are at row no. 66.
No. of elements covered in this row is (50-40) = 10.
Address of A[66][50] = 1000 + (351+10) =1361