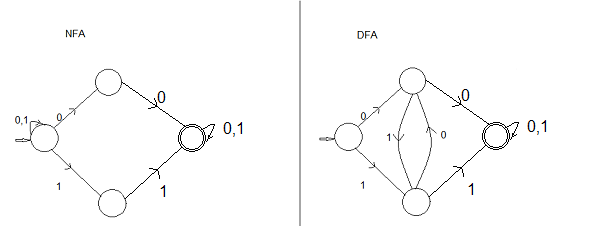
Regular expression says there should be at least 2 consecutive 0's or 2 consecutive 1's.
Construction of finite automata:
Nfa's are usually easy.
1. break down problem and understand requirements. Here we need at least 2 consecutive 0's or 2 consecutive 1's.
2. (0+1)* will accept anything. Whenever you see a '+' try to divide the problem.
Dfa's you can attempt to construct directly for smaller regular expression once you have a good practice.
Here you need to know if 1 is followed by 0 eg. 10 , then you need to keep looking for next immediate(consecutive) 0. Or if you see 0 followed by 1 eg. 01 then you need to search for next immediate(consecutive) 1.
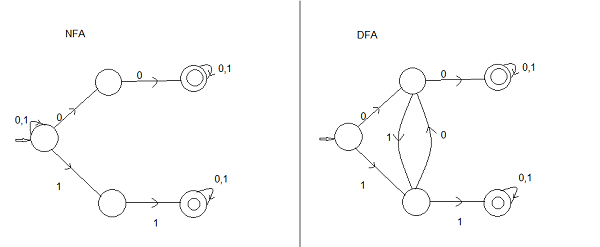
This is not minimum Nfa or Dfa this is just for understanding purpose. You can combine final states to get a minimum one, so in the end both will have four states.
This is a minimized version: