the original image https://drive.google.com/open?id=1-Erqg7Y2xqXJL5YFyDZNh_GJ2Bxto7pT
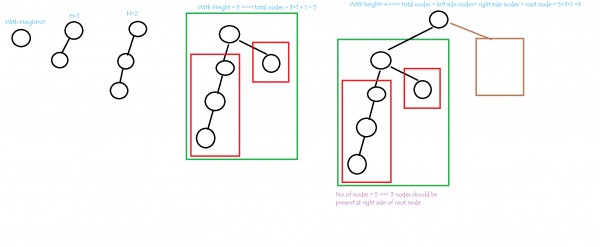
But now i am interested to find it in general height.
we know that the no.of nodes of right side should be less than 2 at maximum only
===> for minimum no.of nodes, i consider no.of right subtree nodes = no.of left subtree nodes - 2
===> Total nodes in that tree = no.of left subtree nodes + no.of right subtree nodes + 1 ( root node)
= no.of left subtree nodes + ( no.of left subtree nodes - 2 ) + 1
= no.of left subtree nodes + no.of left subtree nodes - 2 + 1
= 2 * no.of left subtree nodes - 1
what is no.of nodes in left subtree ?
it should be equal to no.of nodes in h-1, where h is height of your tree
Total nodes in that tree = 2 * no.of left subtree nodes - 1
N(H) = 2 * ( N(H-1) ) - 1
for solving this recurrence relation, the base condition is N(H=3) = 5
using Back Substitution, we an solve it, the final value we can get
N(H) = 4 . 2(H-3) + 1 = 22 . 2(H-3) + 1 = 2(H-3)+2 + 1 = 2(H-1) + 1.