For the given $B^+$ tree, $d = 2 \implies 2d = 4.$ Also right biasing is followed as $69$ is to the right of $69$ in the parent node.
We’ll insert $100$ in the sorted position among the leaf nodes.

This causes an overflow and so the node will split into $2$ by moving the element at position $\left \lceil \dfrac{2d+1}{2}\right \rceil =\left \lceil \dfrac{5}{2} \right \rceil = 3,$ which is $100.$ Thus we get.

This again causes an overflow at the root node and $69$ needs to be moved up forming a new root. Here, $69$ is not a record pointer (only leaf nodes in $B^+$ tree contains record pointers) and so we need not replicate it while moving up.
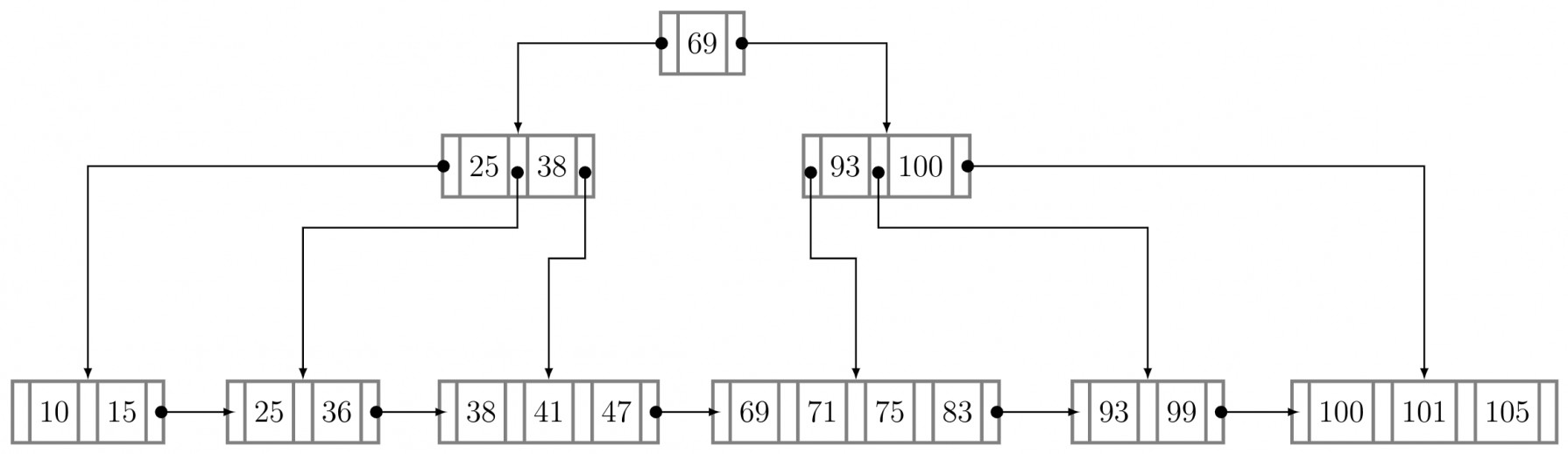
Now all the property of $B^+$ tree is satisfied and the insertion algorithm terminates.