Following must be the correct precedence graph, $S_1$ abd $S_2$ are independent, hence these can be executed in parallel.
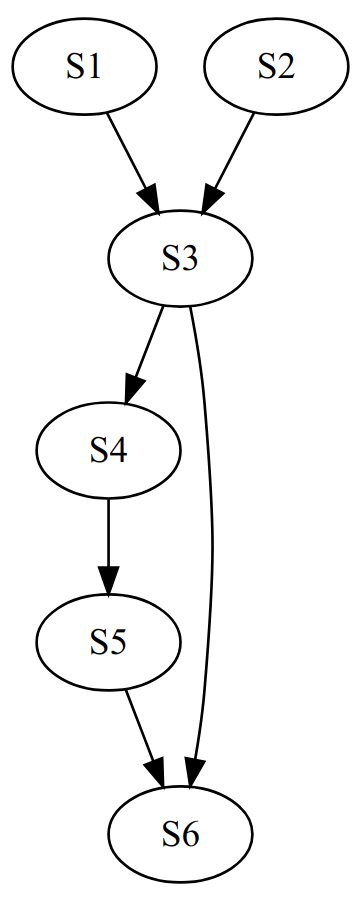
For all those nodes which are independent we can execute them in parallel by creating a separate process for each node like $S_1$ and $S_2$. There is an edge from $S_3$ to $S_6$ it means, until the process which executes $S_3$ finishes its work, we can't start the process which will execute $S_6$.
For more understanding watch the following NPTEL lectures on process management: