A lattice is called a Boolean Algebra, if it is distributive and complemented( if complement exists for every element of lattice).
So, For $2-order$ Boolean Algebra, it's easy to check for these properties to say whether a lattice is boolean Algebra (or) not, But for lattices for higher order (say $3$, $4$ (or) $20$), it becomes worse to Check for distributive properties and finding complement for each element.
One way here would be eliminating options using the property that Every element has a unique complement in a Boolean Algebra
, but the converse is not True.
Any $n-order$ boolean Algebra is isomorphic to any other $n-order$ boolean algebra. And we know that $\color{olive}{\big[ P(A),\subseteq \big]}$ is a boolean Algebra.
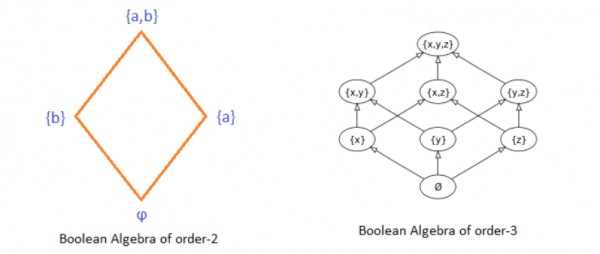
So, any boolean Algebra of $\color{green}{order-2}$ and $\color{green}{order-3}$ must be isomorphic to these two. And also note that a Boolean Algebra of order $n$ has $\color{red}{2^n}$ vertices(nodes) and $\color{red}{n*2^{n-1}}$ edges.
So, now coming to the question the above Hasse diagram is isomorphic to the Boolean Algebra of order-3, Hence it is Boolean Algebra.