For $1$st minimum element there is maximum $0$ comparison
For $2$nd minimum element there is maximum $1$ comparison
For $3$rd minimum element there is maximum $2$ comparison
For $4$st minimum element there is maximum $3$ comparison
...............................................................
For $65$st minimum element there is maximum $64$ comparison
So, total number of comparisons $0+1+2+...+64$
$\frac{64\times 65}{2}=2080$
--------------------------------------------------------------------------------------------------------
Here we operating on min heap and searching for minimum number of comparison. Now, we can compare when atleast $2$ elements in the heap.So, finding minimum element, i.e. at root, we need no comparison
Now, take an example and see for 2nd , 3rd, 4th minimum how many comparison there can be
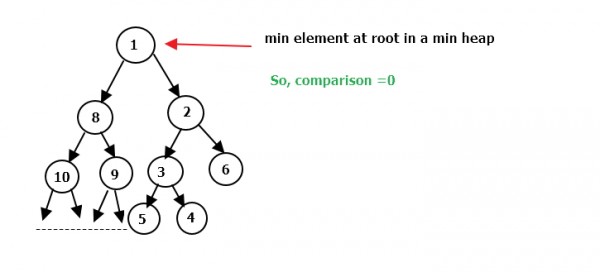
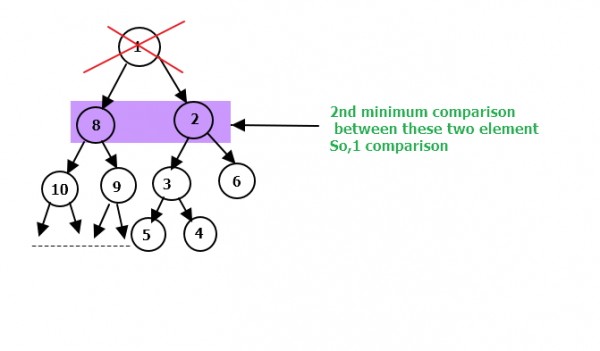

Now, like this way for $4$ th minimum we need comparison between 4,5,6,8 , So, there must be 3 comparison. Now like this if we go for $5$ th minimum there are 4 comparison
So, there will be total $2080$ comparisons
Note: We just operating like this; When got some minimum, we just add it's child for next comparison and remaining element of previous comparison
Say for $2$ nd minimum, we take child of $1$ st minimum
For $3$ rd minimum , we take remaining element of $2$ nd minimum i.e. $8$ and child of $2$ i.e. $3,6$