TIFR CSE 2014 | Part A | Question: 17

Question

A fair dice (with faces numbered $1, . . . , 6$) is independently rolled repeatedly. Let $X$ denote the number of rolls till an even number is seen and let $Y$ denote the number of rolls till $3$ is seen. Evaluate $E(Y |X = 2)$.

• A. $6\frac{5}{6}$
• B. $6$
• C. $5\frac{1}{2}$
• D. $6\frac{1}{3}$
• E. $5\frac{2}{3}$

Comments

5.66

---

Can you explain your approach?

Answer 1

Answer is (E)

$X$: The value of $X$ denotes the number of rolls till an even number is seen.

$Y$:  The value of $Y$ denotes the number of rolls till a $3$ is seen.

For example:

$X = 2$ implies an even number first time occurred on second roll, or outcome of the first roll is odd & outcome of the second roll is even.

$Y = 4$ implies $3$ appeared for first time in the $4^{th}$ die roll.

Ranges of Random Variables $X$ & $Y$

$X:\{ 1, 2, 3,\ldots ,\infty \}$

$Y:\{1, 2, 3,\ldots,\infty \}$ 

$E[Y\mid X = 2]:$ Expected number of rolls till a $3$ is seen given that an even number appeared for the first time in the second roll.

It is sure that $3$ cannot appear on $2^{nd}$ toss, i.e. $P[Y =2\mid X =2] = 0$ and henceforth $E[Y =2\mid X =2] = 0.$

Now, there are two cases possible:

Case 1: 3 appears on the first toss given that outcome of first toss is odd.

i.e., $E[Y = 1\mid X =2]$

Here we need not to concern about outcomes of rolls other than the first roll.

Probability of getting $3$ in first toss given that o/c of the first toss is odd $=P(Y = 1\mid  X = 2)   =\dfrac{1}{3} = 0.33$

So, Expectation $ E[Y = 1\mid X = 2] = y\times P(Y = 1\mid X = 2) =1 \times 0.33 = 0.33$

Case 2: 3 appears on any toss after the second toss given that outcome of first toss is odd, & that of second toss is even

$P[Y = y \mid X = 2]$ = given that $1^{st}$ roll is an odd number and  $2{nd}$ roll is an even number, Probability that out of $y$ rolls,

None of the first $(y – 1)$ roll’s outcome is $3$ &

Outcome of the $y^{th}$ roll is $3$.

So $P[Y = y \mid X = 2] $
$\qquad = \left(\dfrac{2}{3}\right)(\text{for first o/c odd but not } 3)$
$\qquad \times \left(\dfrac{5}{6}\right)^{(y – 3)}( \text{for not getting a} \;3\; from\;3^{rd} \;to\;0 (y – 1)^{th} rolls)$
$\qquad \times \left(\dfrac{1}{6}\right)(\text{for }y^{th} \text{o/c to be}\; 3).$

$P[Y = y \mid X = 2] = \left(\dfrac{2}{3}\right)\times \left(\dfrac{5}{6}\right)^{(y – 3)}\times \left(\dfrac{1}{6}\right)$

So $E[Y = y \mid X = 2]=$ Summation from $y = 3 \text{ to infinity}(y\times P(Y = y \mid X = 2)) = {5.33}$ (where $y\geq 3$)

This summation will give sum of all the expectations from $Y = 3 \text{ to infinity}.$

Now:

Net Expectation is given as:

$E[ Y = y\mid X =2] = E[ Y = 1\mid X = 2] + E[ Y = 2\mid X =2] + E[ Y = y’\mid X =2]$ where $y’\geq 3.$

Putting all the values,

$E[ Y = y\mid X =2] = 0.33 + 0 + 5.33$

So, $E[ Y = y\mid X =2] = 5.66 =\dfrac{17}{3}.$

Comments

I am getting final answer as 5.99 correct if I am wrong you can solve this by arithmetic geometric expression AGP getting answers as 5.66

---

Can someone explain the summation?

---

$Summation\;(S)$

$S=\left(\frac{2}{3}\right)\sum_{y=3}^\infty y\left(\frac{5}{6}\right)^{y-3}\left(\frac{1}{6}\right)$

$9S=\sum_{y=3}^\infty y\left(\frac{5}{6}\right)^{y-3}$

$9S=3+4\left(\frac{5}{6}\right)+5\left(\frac{5}{6}\right)^2+\ldots\to\color{green}{(1)}$

$\color{green}{(1)-(1)}\times\frac{5}{6}$

$9S\left(1-\frac{5}{6}\right)=3+\left(\frac{5}{6}\right)+\left(\frac{5}{6}\right)^2+\left(\frac{5}{6}\right)^3+\ldots$

$\frac{3S}{2}=3+\left(\frac{5/6}{1-5/6}\right)$

$\frac{3S}{2}=8$

$S=16/3=5.33$

Answer 2

Wrong Solution for the unedited question.

Unedited question:

A fair die(with face numbered 1, 2, ....., 6) is independently rolled repeatedly.Let X denote the number is seen & let Y denote the number of rolls till 3 is seen. Evaluate E(Y|X =2)?

A) 41/6

B) 6

C) 11/2

D) 19/3

E) 17/3.

Solution:

I am getting 6 as an APPROXIMATED answer.

This is just an okay method, most probably there must be better & more intuitive solutions to this problem.

X & Y here are random variables. They will contain some values from their ranges of allowed values.

X : The value of X is seen.

Y:  The value of Y denotes the number of rolls till a 3 is seen.

For example:

X = 2 implies 2 is seen,

Y = 4 implies 3 appeared for first time in the 4^th die roll.

Ranges of Random Variables X & Y

X : { 1, 2, 3, 4, 5, 6}

Y: {$1, 2, 3, \ldots\infty$}  

-----------------------------------------------------------------------------------------------------------------

E[Y | X = 2]: the expected (or average) number of rolls till a 3 is seen, given that 2 is seen.

In other words, average number of rolls till 3 appears for the first time in repeated die rolls, given that 2 has been already appeared at least once.

From the definition of Expectation:

$\displaystyle E[Y = y|X = 2] =\sum_{y=1}^{\infty}
{y * P(Y = y | X = 2)}$;

Where  is the probability that 3 appeared for the first time in y^th die roll, given that 2 already has been appeared at least once in the first (y - 1) die rolls.

P( Y = 1|X = 2) = 0,  since there is only one die roll, 3 can't appear after 2.

-----------------------------------------------------------------------------------------------------------

Calculation of P(Y = y|X = 2):

From the definition of conditional probability, for y die rolls:

$P(Y = y | X = 2) = \frac{(P(Y = y) \cap P(X = 2))}{P(X = 2)}$

i.e. $P(Y = y | X = 2) = \frac{\textrm{Probability of first appearance of 3 in the yth roll and  AT LEAST ONE  appearance of 2 in the first (y-1) die rolls}}{\textrm{Probability of at least one appearance of 2 in y die rolls}}$

--------------------------------------------------------------------------------------------------------------

Calculating Denominator: (Probability of at least one appearance of 2 in y die rolls)

$P(Denominator) = \frac{\textrm{Outcomes in which 2 is appearing at least once}}{\textrm{All possible outcomes}}$

$P(Denominator) = \frac{(C_{1}^{y} 6^{(y – 1)} – (y – 1))}{6^y}$

$\textrm{How } (C_{1}^{y} *6^{(y – 1)} – (y – 1))$

Out of y places chose any one place for 2(yC1), in the remaining (y – 1) places any of the 6 outcomes can be placed minus (y -1) repetitions.

----------------------------------------------------------------------------------------------------------------

Calculating Numerator: (Probability of first appearance of 3 in the y^th roll and AT LEAST ONE  appearance of 2 in the first (y-1) die rolls)

$P(Numerator) = \frac{\textrm{Outcomes in which 2 is appearing at least once in first (y-1) rolls and 3 is appearing in the last roll}}{\textrm{All possible outcomes}}$                                    

 $P(Numerator) = \frac{C_{1}^{(y - 1)}5^{(y -2)} – (y-2)}{6^y}$

$\textrm{How } C_{1}^{(y - 1)}5^{(y -2)}– (y-2)$

3 is fixed on the y^th place, out of remaining (y – 1) places chose a place for 2 ((y-1)C1) and fill any of the 5 Outcomes(all possible outcomes EXCEPT 3) in the remaining (y-2) places minus (y -2) repetitions.

---------------------------------------------------------------------------------------------------------------

Now,

$P(Y = y | X =2) = \frac{\textrm{Probability of first appearance of 3 in the y^th roll and AT LEAST ONE  appearance of 2 in the first (y-1) die rolls}}{\textrm{Probability of at least one appearance of 2 in y die rolls}}$

 $P(Y = y | X = 2) = \frac{P(Numerator)}{P(Denominator)}$

On putting the values & simplification,

$P(Y = y | X = 2) = \frac{((y-1)5^{(y-2)}-y+2)}{(y6^{(y-1)}-y+1)}$

By putting the value calculated above, Expectation E[Y | X = 2], can be given as follow:

$ \displaystyle E[Y = y|X = 2] = \sum_{y=2}^{\infty}
y*\frac{((y-1)5^{(y-2)}-y+2)}{(y*6^{(y-1)}-y+1)}$

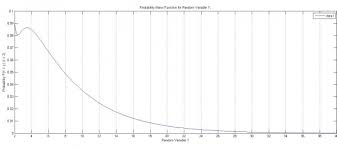
I don’t know how to converge the  Probability Mass Function(P(Y = y|X =2) so I calculated expectation by varying y from 2 to 120(Not Infinity)using fx991ES calculator & got 5.981334741.

I guess, Expectation to be 6.

Here is the plot for a portion of the Probability Mass Function(P(Y = y|X  = 2) in which y is varying from 2 to 40, & weighted average of such a complete graph will give the expectation.

Comments

Thank u anurag for ur explanation.....

Can't we use this approach

No of String with last no is 3 and atleast one 2 =5^(y-1)-4^(y-1)

Here total string possible is 5^(y-1) and I am subtracting all string with no 2 at any of this y-1 pos we are restricted to use 3 already and now 2 also means 4^(y-1)

Total no of string with atleast 2 appear once is 6^(y) - 5^(y)

So PMF will be {y (5^(y-1)- 4^(y-1))/(6^y-5^y)} please correct me if I am thinking in wrong direction

---

Exactly! you are right Saurav.

I got the same PMF after correction,

& even the blue line in my previous comment is the plot for that PMF.

& this PMF will give the value of expectation for that unedited question near about 5.75

---

I am getting final answer as 5.99 correct if I am wrong you can solve this by arithmetic geometric expression AGP getting answers as 5.66 so final answer hai approximated to 6 hai

Answer 3

$X = \# \text{Rolls till even number is seen}$

$Y = \# \text{Rolls till number 3 shows up}$

We need to find $\mathbb{E}(Y \ | \ X = 2)$

---

$$\begin{align}
\mathbb{E}(Y \ | \ X = 2) &= \sum_{y=0}^{\infty} yP(Y=y \ | \ X=2) \\ 
&= \sum_{y=0}^{\infty} y \dfrac{P(Y=y, X=2)}{P(X=2)} = \sum_{y=0}^{\infty} y \dfrac{P(Y=y, X=2)}{\underbrace{\frac{3}{6}}_{\text{No even number}}.\underbrace{\frac{3}{6}}_{\text{| Only even number}}}
\end{align}$$

$\underline{\textbf{Observation(s)}}$

$P(Y=2, X=2) = 0$, since at second roll we having even number as $X=2$, and $3$ is odd, hence $3$ can't show up on the second roll as $Y=2$ is indicating. 

---

$$\begin{align}
\mathbb{E}(Y \ | \ X=2) &= 4 \Big[0.P(Y=0, X=2) + 1.P(Y=1, X=2) + 3.P(Y=3, X=2) + \dots\Big]\\
&=  4\Big[1.\underbrace{\frac{1}{6}}_{\{3\}}.\underbrace{\frac{3}{6}}_{\{2,4,6\}} + 3.\underbrace{\frac{2}{6}}_{\{1,3,5\}-\{3\}}.\underbrace{\frac{3}{6}}_{\{2,4,6\}}.\underbrace{\frac{1}{6}}_{\{3\}} + 4.\frac{2}{6}.\frac{3}{6}.\underbrace{\frac{5}{6}}_{\substack{\{1,2,4,5,6\}}}.\frac{1}{6} + 5.\frac{2}{6}\frac{3}{6}\frac{5}{6}\frac{5}{6}\frac{1}{6}+\dots\Big]\\
&= 4 \Big[1.\frac{1}{12} + 3.\frac{1}{36} + 4.\frac{1}{36}.\frac{5}{6} + 5.\frac{1}{36}.\Big(\frac{5}{6}\Big)^2 + 6.\frac{1}{36}.\Big(\frac{5}{6}\Big)^3 + \dots\Big] \\ 
&= 4 \Bigg[\frac{1}{12} + \frac{1}{36} \underbrace{\Big[3 + 4.\Big(\frac{5}{6}\Big)^1 + 5.\Big(\frac{5}{6}\Big)^2 + 6.\Big(\frac{5}{6}\Big)^3 + \dots\Big]}_{AGP}\Bigg]\\
&= 4 \Bigg[\frac{1}{12} + \frac{1}{36}\Big[48\Big]\Bigg]\\
&= \frac{17}{3} = 5\frac{2}{3}
\end{align}$$

$\textbf{Option (E) is correct}$

---

$\underline{\textbf{AGP Solution}}$

Suppose you have a series $a, (a+d)r, (a+2d)r^2, (a+3d)r^3, \dots$

Then sum of this series is given by $\dfrac{a}{1-r} + \dfrac{dr}{(1-r)^2}$

Above we are having $a=3, d=1, r=\frac{5}{6}$