Answer is E. The catch here is edge-weights belongs to real number. Therefore, edge weight can be negative. In that case the minimum spanning tree may be different.
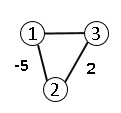
$T$ is:

New edge weights:
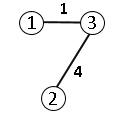
EDIT:
(Here every edge weight is distinct, therefore MST is unique.)
Option A is True. If we apply Kruskal's algorithm, it will choose $e_1$
Option B is True. If we apply Kruskal's algorithm then it will also choose $e_2$, and $2$ edges can not form a cycle. ($e_3$ is not guaranteed in MST, as it may form a cycle)
Option C is also true. If we apply Prims algorithm also on any vertex (say u), it chooses minimum
weight edge incident on vertex u.
Option D is true. Because every edge weight is distinct.