Option (C) is correct. Reason is as follows :
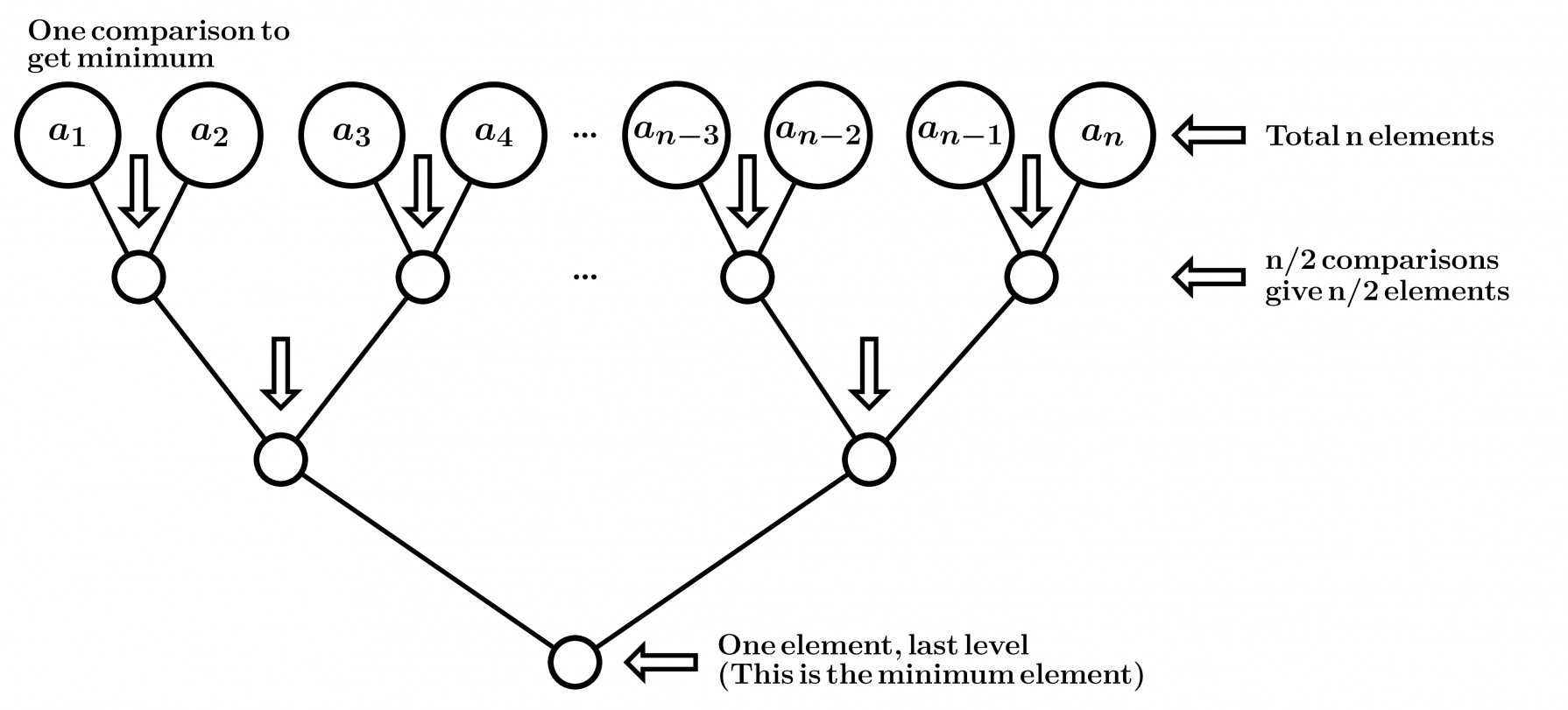
Here, at first level we are Given $n$ elements, out of which we have to find smallest $3$ numbers.
We compare $2 -2$ elements as shown in figure & get $n/2$ elements at Second level.
Note: Minimum element is in these $n/2$ elements.
So, comparisons for this is $n/2$.
Similarly for next level we have $n/4$ Comparisons & $n/2$ elements and so on.
Total Comparisons till now is $n/2 + n/4 + n/8 + \ldots + 4 + 2 +1 = (2^{\log n}-1) = n-1$ {Use G.P. sum}
Now we have to get smallest $3$.
We have 1st smallest at last level already =>$0$ Comparison for this.
=> $2^{nd}$ and $3^{rd}$ smallest elements can be found in $O(\log n)$ time as shown below:
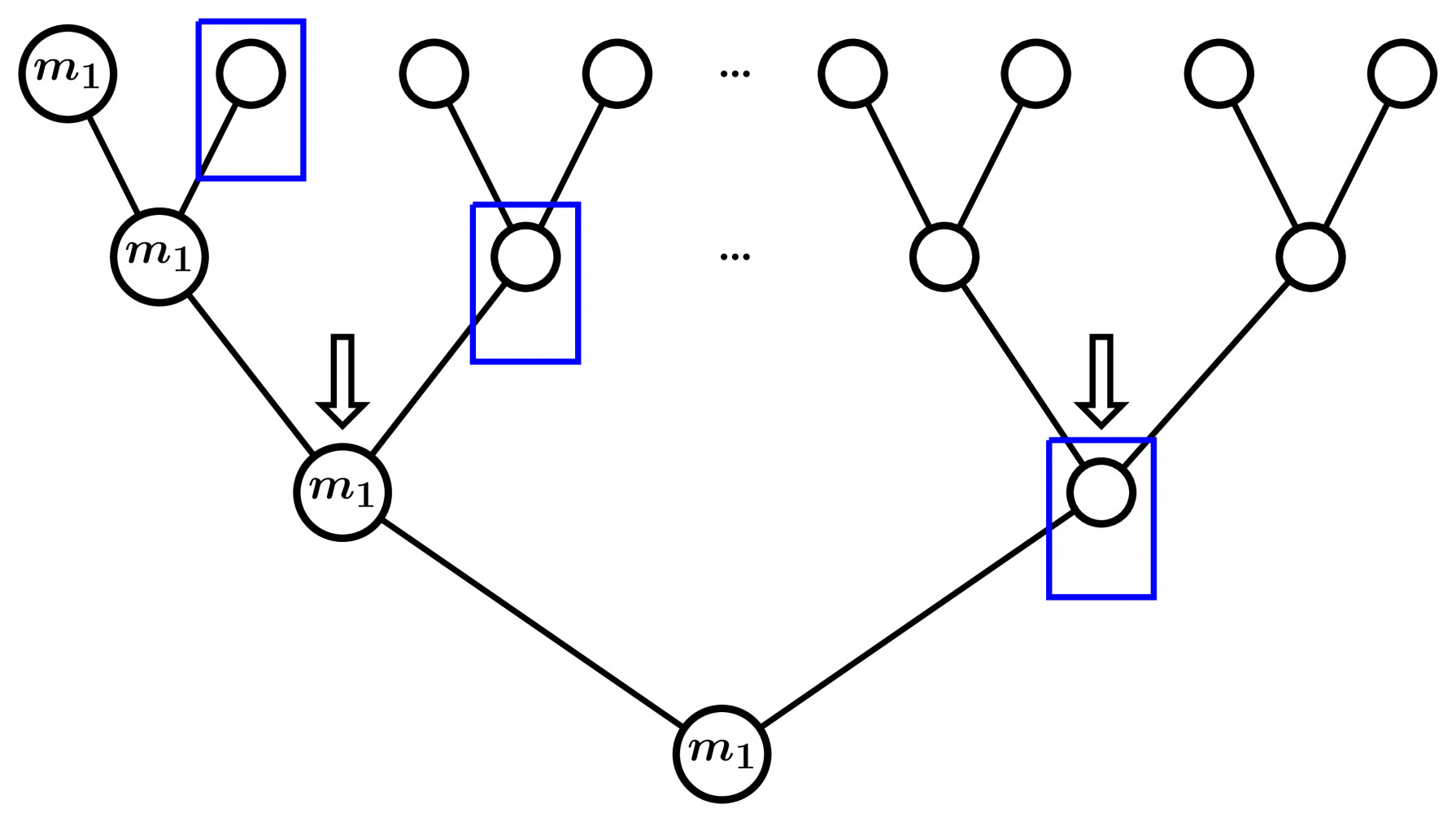
Minimum Element must have descended down from some path from top to Bottom.
SQUARES represent Candidates for $2^{nd}$ minimum.
Every element that is just below $m_1$ (first minimum) is a candidate for second minimum.
So, $O(\log n)$ Comparisons for finding second smallest.
Similarly for $3^{rd}$ minimum we get $O(\log n)$ time. As every element that is just below 1st & 2nd minimum is a candidate for $3^{rd}$ minimum.