Generating Function

Question

What will be solution of this function for coefficient of $x^{100}$?

$$\frac{1}{\left ( 1-x^{10} \right )(1-x^{20})(1-x^{50})}$$

Comments

@akash.dinkar12

plz explain more

I havenot got it

---

In the answer section, someone has written f(x) right!! u can come to this expansion easily by binomial theorem...Then from each of three expansion, u can fetch out powers of x

for eg: 1 1 x100  or 1 x100  1   or  x100 1 1

           x20 x80  1 or x80 x20 1

---

Is it 10?

Answer 1

$[x^{100}] \ \ \ \ \ \ \ \ \  \ $$\Large \frac{1}{\left ( 1-x^{10} \right )(1-x^{20})(1-x^{50})}$

 

$[x^{100}] \ \ \ \ \ \ \ \ \  \ $ $(1-x^{10})^{-1}$$(1-x^{20})^{-1}$$(1-x^{50})^{-1}$

 

$= \Large \color{red} {\binom{-1}{10}\binom{-1}{0}\binom{-1}{0} + \binom{-1}{0}\binom{-1}{5}\binom{-1}{0} + \binom{-1}{0}\binom{-1}{0}\binom{-1}{2}}+ \color{blue}{ \binom{-1}{8}\binom{-1}{1}\binom{-1}{0} + \binom{-1}{6}\binom{-1}{2}\binom{-1}{0} + \binom{-1}{4}\binom{-1}{3}\binom{-1}{0} + \binom{-1}{2}\binom{-1}{4}\binom{-1}{0} } + \color{Orange}{ \binom{-1}{5}\binom{-1}{0}\binom{-1}{1} } + \color{maroon}{\binom{-1}{3}\binom{-1}{1}\binom{-1}{1} + \binom{-1}{1}\binom{-1}{2}\binom{-1}{1} } $

 

$\Large \large \binom{-n}{k} = \binom{n + k - 1}{k}$

So after calculating all the terms for each term we get $1$ and there are 10 such terms above 

So coefficient of $x^{100}$ is $10$

---

There are many terms so to differentiate among them distinct colors are used

1. $\color{red}{\text{Red}}$ - Selecting x from any one of $(1-x^{10})^{-1}$$(1-x^{20})^{-1}$$(1-x^{50})^{-1}$
2. $\color{Blue}{\text{Blue}}$ - Selecting from both $(1-x^{10})^{-1}$$(1-x^{20})^{-1}$
3. $\color{Orange}{\text{Orange}}$ - Selecting from both $(1-x^{10})^{-1}$$(1-x^{50})^{-1}$
4. $\color{maroon}{\text{Maroon}}$ - Selecting from all $(1-x^{10})^{-1}$$(1-x^{20})^{-1}$$(1-x^{50})^{-1}$

Comments

@Mk Utkarsh

I am getting coeff. as 9. Can you please verify my mistake.

$(1+x^{10}+x^{20}+x^{30}+....)*(1+x^{20}+x^{40}+x^{60}+....)(1+x^{50}+x^{100}+x^{150}+....)$

Consider them in the power of x:

$(1+10+20+30+40+50+60+70+80+90+100)*(1+20+40+60+80+100)*(1+50+100)$

$(1+10+20+30+40+50+60+70+80+90+100)*(1+20+40+50+60+70+80+90+100)$

$=9x^{100}$

$=9$

---

Edited:

Mistake verified by @utkarsh

$(1+10+20+30+40+50+60+70+80+90+100)*(1+20+40+50+60+70+80+90+100+\fbox{100})$

$=10x^{100}$

$=10$

Answer 2

Brute Force 

$f(x)=(1+x^{10}+x^{20}+...)*(1+x^{20}+x^{40}+...)*(1+x^{50}+x^{100}+...)$

So, the tuples $<p,q,r>$ where $p,q,r$ belong to $1^{st},2^{nd},3^{rd}$ expression in right hand side which makes for coefficient $100$ are $10$ in number. therefore $10$ (Thanks @akash.dinkar12 for correct number. Earlier miscalculated to $7$)

Tuples are = {<0,0,100>, <100,0,0>,<0,100,0>,<30,20,50>,<10,40,50>,<50,0,50>,<20,80,0>,<40,60,0>,<60,40,0>,<80,20,0>}.

 

Answer 3

This is an amazing question! After reading a lot on math.exchange and especially this paper, https://arxiv.org/pdf/1312.7147.pdf, this is a classic problem called coefficients of Sylvester’s denumerant. 

First of here's the expansion from Wolfram so that you can verify. 

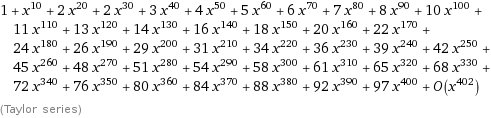
Here's the shortcut!

So, it's straightforward the coefficient of $x^{100}$ is $10$.

Now let me explain in a simple way how to solve these for three coins. ( Full credit to this paper, https://arxiv.org/pdf/1406.5213.pdf, though note, this paper explains for 4 coins of different denominations.)

Define, $$S = \{i, s, t\} $$ which is a set containing the coins (denominations). For our problem, $i = 10, s = 20, t = 50$

So, for us,

$$S = \{ 10,20,50 \}$$

Let me denote $c_n$ as the coefficient to find for $x^n$ defined in the paper as a recurrence relation,

$$c_n = b_n + c_{n-t}$$ 

note here, $c_n = 0$ if $n \leq -1.$ ( I proved this by using Point 2, Def 2.2 in Page 3 ), and $c_0 = 1$, just substitute $n=0$ in the relation above.

 

Now, Theorem 1:

 $$(\forall n) b = \left\lfloor\dfrac{n}{s}\right\rfloor + 1 $$

That's it!

---

Now you can solve any question using this. Let's go with our question and then two examples to clear out.

So, we need to find $c_{100}$. ( here, $s = 20, t = 50$ )

$$c_{100} = b_{100} + c_{100-50} = b_{100} + c_{50}$$

$$b_{100} = \left\lfloor\dfrac{n}{s}\right\rfloor + 1 = \left\lfloor\dfrac{100}{20}\right\rfloor +1 = 5 + 1 = 6$$

So, 

$$c_{100} = 6 + c_{50}$$ 

Now, 

$$c_{50} = b_{50} + c_0$$

$$b_{50} = \left\lfloor\dfrac{50}{20}\right\rfloor + 1 = 3$$

So we have now, 

$$c_{50} = b_{50} + c_0 = 3 + 1 = 4$$

Thus, 

$$c_{100} = 6 + 4$$

$$c_{100} = 10$$

...which is our coefficent!

---

Let's take another example, find the coeffient of $x^{160}$ in the above expansion. Checking the Wolfram brute force method it's $20$.

Same as usual, ( I'm skipping obvious steps now, it's too long to write now, :P )

$$c_{160} = b_{160} + c_{160-50} = b_{160} + c_{110}$$

We know, $b_{160} = 9$

$$c_{110} = b_{110} + c_{60}$$

Again, $b_{110} = 6$

$$c_{60} = b_{60} + c_{10}$$

Here,  $b_{60} = 4$

$$c_{10} = b_{10} + c_{-40}$$

Note, $b_{10} = \left\lfloor\dfrac{10}{20}\right\rfloor + 1 = 0 + 1 = 1$ and $c_{-40} = 0$ 

So, $c_{10} = 1$

So, $$c_{160} = b_{160} + c_{160-50} = b_{160} + c_{110}$$

$$ = c_{160} = 9 +  6 + 4 + 1$$

$$c_{160} = 20$$

...which fits the brute force method. 

---