Let $G$ be a finite group of order $k$
then every element of $G$ will have order $m$ such that $k \ \text{mod } m = 0$
A is true because $8 \ \text{mod } 6 = 2$
B is false because $8 \ \text{mod } 4 = 0$ but it is not necessary that there must exist an element with order 4.
for example Elementary abelian group:E8 is of order 8 but does not contain any element of order 4
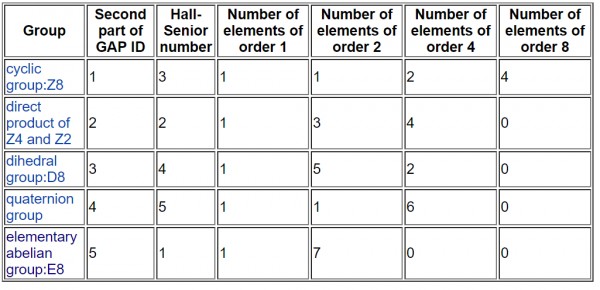
C is false because there must exist only 1 identity element in a group