Let $G$ be the directed, weighted graph shown in below figure
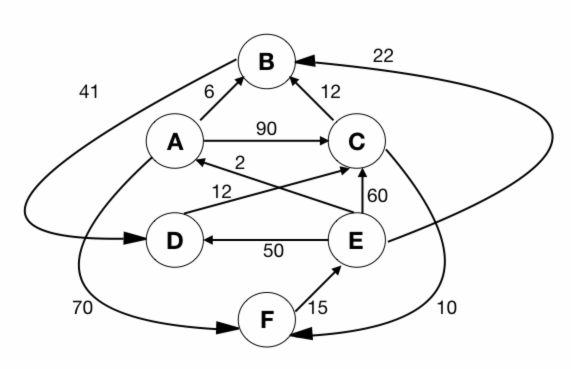
We are interested in the shortest paths from $A$.
-
Output the sequence of vertices identified by the Dijkstra’s algorithm for single source shortest path when the algorithm is started at node $A$
-
Write down sequence of vertices in the shortest path from $A$ to $E$
-
What is the cost of the shortest path from $A$ to $E$?